题目内容
8.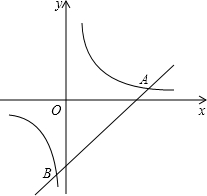 如图,已知一次函数y1=x-6与反比例函数y2=$\frac{7}{x}$的图象交于A、B两点.
如图,已知一次函数y1=x-6与反比例函数y2=$\frac{7}{x}$的图象交于A、B两点.(1)求A、B两点的坐标;
(2)如果y1-y2>0,根据图象直接写出x的取值范围.
分析 (1)根据两个函数的解析式可得x-6=$\frac{7}{x}$,求得x的值,进而求得点的坐标;
(2)y1-y2>0,即y1>y2,即一次函数的图象在反比例函数的图象的上边的未知数的取值范围.
解答 解:(1)解方程x-6=$\frac{7}{x}$,
得x1=7,x2=-1,
∴A(7,1)、B(-1,-7);
(2)y1-y2>0,即y1>y2,由图象知-1<x<0,或x>7.
点评 本题综合考查一次函数与反比例函数的图象与性质,同时考查用待定系数法求函数解析式.本题需要注意无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;需注意反比例函数的自变量不能取0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.估计$\sqrt{76}$的大小应在( )
| A. | 7与8之间 | B. | 8.0与8.5之间 | C. | 8.5与9.0之间 | D. | 9与10之间 |
20. 一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了( )
一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了( )
 一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了( )
一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了( )| A. | 1.5米 | B. | 0.9米 | C. | 0.8米 | D. | 0.5米 |
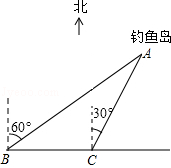 如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行50海里与钓鱼岛A的距离最近?
如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行50海里与钓鱼岛A的距离最近?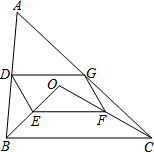 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.