题目内容
11.把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=6,则AD=3$\sqrt{2}$.分析 由于矩形DMNC与矩形ABCD相似,根据相似三角形对应边的比相等,就可以得到AD的长.
解答 解:由已知得MN=AB,MD=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∵矩形DMNC与矩形ABCD相似,
∴$\frac{DM}{AB}$=$\frac{MN}{BC}$,
∵MN=AB,DM=$\frac{1}{2}$AD,BC=AD,
∴$\frac{1}{2}$AD2=AB2,
∴由AB=6得,AD=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 本题考查相似多边形的性质,熟练掌握相似三角形对应边的比相等的性质是解题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 如图,△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,点D、E分别为AM、AB的动点,则BD+DE的最小值是8.
如图,△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,点D、E分别为AM、AB的动点,则BD+DE的最小值是8.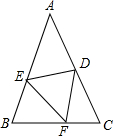 如图,已知△ABC中,AB=AC=6,BC=4,点D,E,F分别在AC,AB,BC边上,△BEF沿着直线EF翻折后与△DEF重合,若△DFC与△ABC相似,则CD的长为$\frac{6}{5}$或$\frac{4}{5}$.
如图,已知△ABC中,AB=AC=6,BC=4,点D,E,F分别在AC,AB,BC边上,△BEF沿着直线EF翻折后与△DEF重合,若△DFC与△ABC相似,则CD的长为$\frac{6}{5}$或$\frac{4}{5}$. 已知一次函数y=kx+b的图象如图所示:
已知一次函数y=kx+b的图象如图所示: