题目内容
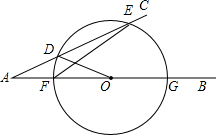 如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF.若∠BAC=24°,则∠EFG=
如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF.若∠BAC=24°,则∠EFG=考点:圆周角定理
专题:
分析:连接OE,利用三角形的外角性质得出∠ODC的度数,再求出∠DOC,从而求出∠EOG的度数,再利用圆周角定理求出∠EFG的度数.
解答: 解:连接EO,
解:连接EO,
∵AD=DO,
∴∠BAC=∠DOA=24°,
∴∠EDO=48°,
∵DO=EO,
∴∠OED=∠ODE=48°,
∴∠DOE=180°-48°-48°=84°,
∴∠EOG=180°-84°-24°=72°,
∴∠EFG=
∠EOG=36°,
故答案为:36°.
 解:连接EO,
解:连接EO,∵AD=DO,
∴∠BAC=∠DOA=24°,
∴∠EDO=48°,
∵DO=EO,
∴∠OED=∠ODE=48°,
∴∠DOE=180°-48°-48°=84°,
∴∠EOG=180°-84°-24°=72°,
∴∠EFG=
| 1 |
| 2 |
故答案为:36°.
点评:此题主要考查了圆周角定理,三角形外角的性质的综合运用,做题的关键是理清角之间的关系.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
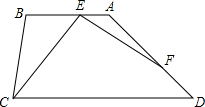 如图,梯形ABCD,AB与CD平行,∠BCD=2∠D=2α,∠CEF=∠B,
如图,梯形ABCD,AB与CD平行,∠BCD=2∠D=2α,∠CEF=∠B,