题目内容
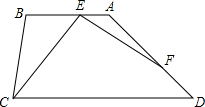 如图,梯形ABCD,AB与CD平行,∠BCD=2∠D=2α,∠CEF=∠B,
如图,梯形ABCD,AB与CD平行,∠BCD=2∠D=2α,∠CEF=∠B,(1)用α表示∠CEF=
(2)当AB=BC时,猜想EC、EF的数量关系,并证明.
考点:全等三角形的判定与性质
专题:
分析:(1)证明∠B+∠BCD=180°,而∠BCD=2α,即可解决问题.
(2)如图,作辅助线;证明A、E、C、F四点共圆,进而证明∠ECF=∠EFC,问题即可解决.
(2)如图,作辅助线;证明A、E、C、F四点共圆,进而证明∠ECF=∠EFC,问题即可解决.
解答: 解:(1)∵AB∥CD,
解:(1)∵AB∥CD,
∴∠B+∠BCD=180°,而∠BCD=2α,
∴∠CEF=∠B=180°-2α.
(2)猜想:EC=EF.证明如下:
如图,连接AC,CF;
∵AB∥CD,
∴∠BAC=∠ACD;而AB=BC,
∴∠BAC=∠BCA=β,
∴∠BCA=∠ACD=β,
即∠BCD=2∠ACD,而∠BCD=2∠D,
∴∠ACD=∠D=β;
由三角形的内角和定理得:∠B=∠CAD=180°-2β,
而∠CEF=∠B,
∴∠CEF=∠CAF,
∴A、E、C、F四点共圆,
∴∠EFC=∠BAC=β,∠ECF+∠A=180°;
∵AB∥CD,
∴∠D+∠A=180°,
∴∠ECF=∠D=β,
∴∠ECF=∠EFC,
∴EC=EF.
 解:(1)∵AB∥CD,
解:(1)∵AB∥CD,∴∠B+∠BCD=180°,而∠BCD=2α,
∴∠CEF=∠B=180°-2α.
(2)猜想:EC=EF.证明如下:
如图,连接AC,CF;
∵AB∥CD,
∴∠BAC=∠ACD;而AB=BC,
∴∠BAC=∠BCA=β,
∴∠BCA=∠ACD=β,
即∠BCD=2∠ACD,而∠BCD=2∠D,
∴∠ACD=∠D=β;
由三角形的内角和定理得:∠B=∠CAD=180°-2β,
而∠CEF=∠B,
∴∠CEF=∠CAF,
∴A、E、C、F四点共圆,
∴∠EFC=∠BAC=β,∠ECF+∠A=180°;
∵AB∥CD,
∴∠D+∠A=180°,
∴∠ECF=∠D=β,
∴∠ECF=∠EFC,
∴EC=EF.
点评:该题以梯形为载体,以平行线的性质、等腰三角形的判定、四点共圆的判定及其应用等几何知识点为考查的核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
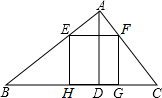 已知△ABC中,BC=8,AD是BC上的高,AD=12,E、F分别在AB、AC上滑动(不与点B、C重合),且EF∥BC,以EF为一边作△ABC的内接矩形EFGH.求:
已知△ABC中,BC=8,AD是BC上的高,AD=12,E、F分别在AB、AC上滑动(不与点B、C重合),且EF∥BC,以EF为一边作△ABC的内接矩形EFGH.求: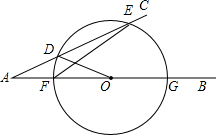 如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF.若∠BAC=24°,则∠EFG=
如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF.若∠BAC=24°,则∠EFG=
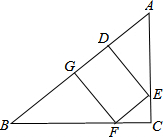 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,在线段AB上取一点D,过D作DE⊥AB交AC于E,过E作EF⊥DE交BC于F,过F作FG⊥EF交AB于G,得到矩形DEFG.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,在线段AB上取一点D,过D作DE⊥AB交AC于E,过E作EF⊥DE交BC于F,过F作FG⊥EF交AB于G,得到矩形DEFG.