题目内容
5.(1)已知(x+2)2+|y+1|=0,求x,y的值;(2)化简:$\frac{3}{4}{x^2}y-[\frac{1}{2}xy+\frac{1}{3}(\frac{1}{2}{x^2}y-9xy)]$.
分析 (1)由偶次方和绝对值的非负性质即可得出结果;
(2)根据去括号法则先去小括号,再去中括号,然后合并同类项即可.
解答 解:(1)∵(x+2)2+|y+1|=0,
∴x+2=0,y+1=0,
∴x=-2,y=-1;
(2)$\frac{3}{4}{x^2}y-[\frac{1}{2}xy+\frac{1}{3}(\frac{1}{2}{x^2}y-9xy)]$
=$\frac{3}{4}{x}^{2}y$-[$\frac{1}{2}$xy+$\frac{1}{6}$x2y-3xy]
=$\frac{3}{4}{x}^{2}y$-$\frac{1}{2}$xy-$\frac{1}{6}$x2y+3xy
=$\frac{7}{12}$x2y+$\frac{5}{2}$xy.
点评 本题考查了偶次方和绝对值的非负性质、整式的加减法法则、去括号法则、合并同类项;熟记偶次方和绝对值的非负性质、去括号法则、合并同类项是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.雾霾天气严重影响市民的生活质量.在去年寒假期间,某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民.并对调查结果进行了整理.绘制了如图不完整的统计图表.观察分析并回答下列问题.
(1)本次被调查的市民共有多少人?
(2)求m、n的值,并计算图2中区域B所对应的扇形圆心角的度数;
(3)若该市有100万人口,请估计持有A、B两组主要成因的市民有多少人?

| 组别 | 雾霾天气的主要成因 | 百分比 |
| A | 工业污染 | 45% |
| B | 汽车尾气排放 | m |
| C | 炉烟气排放 | 15% |
| D | 其他(滥砍滥伐等) | n |
(2)求m、n的值,并计算图2中区域B所对应的扇形圆心角的度数;
(3)若该市有100万人口,请估计持有A、B两组主要成因的市民有多少人?

14. 已知二次函数y=x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )
已知二次函数y=x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )
 已知二次函数y=x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )
已知二次函数y=x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )| A. | -1<x<3 | B. | -1<x<4 | C. | x<-1或x>3 | D. | x<-1或x>4 |
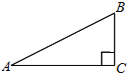 如图,在Rt△ABC中,∠ABC=90°,BC=1,AC=$\sqrt{5}$.
如图,在Rt△ABC中,∠ABC=90°,BC=1,AC=$\sqrt{5}$.
 如图图形中对称轴最多的是圆.
如图图形中对称轴最多的是圆. 如图,已知点D、E是△ABC的边BC上两点,且BD=CE,∠1=∠2.试证:△ABC是等腰三角形.
如图,已知点D、E是△ABC的边BC上两点,且BD=CE,∠1=∠2.试证:△ABC是等腰三角形. 如图,△ABC中,AD是高,E、F分别是AB、AC的中点.若AB=10,AC=8,则四边形AEDF的周长为18.
如图,△ABC中,AD是高,E、F分别是AB、AC的中点.若AB=10,AC=8,则四边形AEDF的周长为18.