题目内容
2.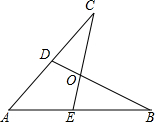 如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC.
如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC.
分析 由三角形全等的判定方法SAS、ASA、AAS,容易得出结论.
解答 解:AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC;理由如下:
若AD=AE,
在△ACE和△ABD中,$\left\{\begin{array}{l}{AC=AB}&{\;}\\{∠A=∠A}&{\;}\\{AE=AD}&{\;}\end{array}\right.$,
∴△ACE≌△ABD(SAS);
若CD=BE,
∵AB=AC,
∴AD=AE,
同理:△ACE≌△ABD(SAS);
若∠B=∠C,
在△ACE和△ABD中,$\left\{\begin{array}{l}{∠A=∠A}&{\;}\\{AC=AB}&{\;}\\{∠C=∠B}&{\;}\end{array}\right.$,
∴△ACE≌△ABD(ASA);
若∠ADB=∠AEC,
在△ACE和△ABD中,$\left\{\begin{array}{l}{∠A=∠A}&{\;}\\{∠AEC=∠ADB}&{\;}\\{AC=AB}&{\;}\end{array}\right.$,
∴△ACE≌△ABD(AAS);
故答案为:AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC.
点评 本题考查了全等三角形的判定方法;本题是开放型题目,存在四种情况,熟练掌握全等三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目
10.已知两圆的半径是4和5,圆心距满足不等式组$\left\{\begin{array}{l}{x+2>\frac{x+5}{2}}\\{5x-4<2x+23}\end{array}\right.$,则两圆的位置关系是( )
| A. | 相交 | B. | 外切 | C. | 内切 | D. | 外离 |
14.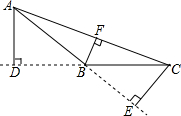 如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )
如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )
 如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )
如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )| A. | $\frac{12}{5}$ | B. | 3 | C. | 4 | D. | 5 |
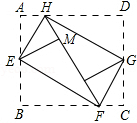 如图,将长方形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的长方形EFGH.若AE=3,FH=7,则原长方形的面积为42.
如图,将长方形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的长方形EFGH.若AE=3,FH=7,则原长方形的面积为42. 如图,AD是△ABC的中线.
如图,AD是△ABC的中线.