题目内容
17.如图1,在平面直角坐标系中,直线y=x+6与x轴交于点A,与y轴交于点B.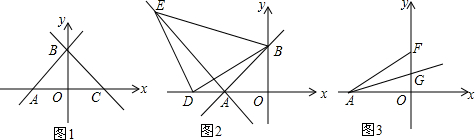
①如图2,若过点B作直线BC使得BC⊥AB于点B,且交x轴于C,求△ABC的面积.
②D为线段OA延长线上一动点,在第二象限内以BD为直角边做等腰直角三角形BDE,连结EA.求直线EA的函数表达式.
③如图3,点F是y轴正半轴上一点,且F点坐标为(0,2$\sqrt{3}$),AG平分∠OAF,点M是射线AG上一动点,点N是线段AO上一动点,试判断是否存在这样的点M、N,使得OM+MN的值最小?若存在,请写出其最小值,并加以说明.
分析 ①根据直线与坐标轴的交点易得A,B两点坐标,然后根据三角形面积公式计算;
②过点E作x轴的垂线EM交x轴点M,根据全等三角形的判定和直线解析式的解答即可;
③根据勾股定理进行解答即可.
解答 解:①由题意可得:A点坐标为(-6,0),B点坐标为(0,6),
则△AOB为等腰直角三角形,
∵BC⊥AB,
∴△ABC为等腰直角三角形且AC=12,
∴S△ABC=36;
②过点E作x轴的垂线EM交x轴点M,如图1: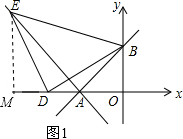 .
.
设线段DA=a,则DO=6+a,
∵△EDB为等腰直角三角形,
∴ED=DB且∠EDB=90°,
∴∠EDM+∠BDO=90°,
易得:∠EDM=∠DBO,∠EMD=∠BOB=90°,
∴△EMD≌△DOB,
∴EM=DO=6+a,MD=BO=6,
$\begin{array}{l}∵点M,D在x轴负半轴上,点E在第二象限内\\∴点E的坐标为(-12-a,6+a)\end{array}$
设经过A,E两点的直线解析式为y=kx+b则有:
$\left\{\begin{array}{l}-6k+b=0\\(-12-a)k+b=6+a\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-1}\\{b=-6}\end{array}\right.$,
直线EA的解析式为y=-x+6;
③线段AO,射线AG上分别任取点N,M作点N关于射线AG对称的点N',由题意可知点N'落在AF上,要使得OM+MN的值最小则需要点O,M,N'三点共线且ON'⊥AF,如图2: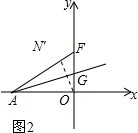
由勾股定理得$AF=4\sqrt{3}$,
${S_{△AOE}}=\frac{1}{2}AO*OF=\frac{1}{2}AF*ON'$
则有:ON'=3,
因此OM+MN的最小值为3.
点评 本题考查了一次函数的综合题,关键是根据直线与坐标轴的交点易得A,B两点坐标进行解答.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案| A. |  | B. |  | C. |  | D. |  |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
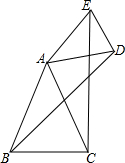 已知如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,求证:∠ABD=∠ACE.
已知如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,求证:∠ABD=∠ACE.