题目内容
7.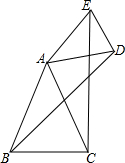 已知如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,求证:∠ABD=∠ACE.
已知如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,求证:∠ABD=∠ACE.
分析 先求出∠EAC=∠DAB,再利用“边角边”证明△AEC≌△ADB,即可得到∠ABD=∠ACE.
解答 解:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠EAC=∠DAB,
在△AEC和△ADB中$\left\{\begin{array}{l}{AD=AE}\\{∠DAB=∠EAC}\\{AB=AC}\end{array}\right.$,
∴△AEC≌△ADB(SAS).
∴∠ABD=∠ACE.
点评 本题考查了全等三角形的判定,推出∠EAC=∠DAB是解题的关键,本题图形比较复杂,准确识图非常重要.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
15.反比例函数y=$\frac{{k}^{2}}{x}$(k为常数,k≠0)的图象位于第( )象限.
| A. | 一、三 | B. | 二、三 | C. | 一、四 | D. | 二、四 |
19.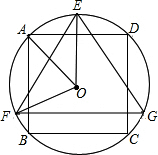 如图,△EFG是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥FG,则∠AOF的度数是( )
如图,△EFG是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥FG,则∠AOF的度数是( )
 如图,△EFG是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥FG,则∠AOF的度数是( )
如图,△EFG是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥FG,则∠AOF的度数是( )| A. | 60° | B. | 65° | C. | 72° | D. | 75° |