题目内容
8.已知二次函数y=x2+bx+c的图象经过A(0,1),对称轴x=2.(1)求b和c的值;
(2)抛物线顶点为P,与x轴交于M,N,求△PMN的面积.
分析 (1)首先由对称轴方程x=2,可求出b的值,再把点A的坐标代入可求出c的值;
(2)根据抛物线的解析式可得出抛物线的顶点坐标和M、N的坐标,即可得出MN的长,然后以P点纵坐标的绝对值为高即可求得三角形PMN的面积.
解答 解:(1)∵抛物线的对称轴是x=2,
∴-$\frac{b}{2}$=2,
解得:b=-4,
∵二次函数y=x2+bx+c的图象经过A(0,1),
∴c=1;
(2)由(1)可知:y=x2-4x+1,
∴M(2+$\sqrt{3}$,0),N(2-$\sqrt{3}$,0),
∴MN=2$\sqrt{3}$,
∵y=x2-4x+1=(x-2)2-5,
已知P(2,-5).
S△PMN=$\frac{1}{2}$×2$\sqrt{3}$×5=5$\sqrt{3}$.
点评 本题考查了二次函数解析式的确定、抛物线和坐标轴的交点、图形面积的求法以及三角形面积公式的运用,熟记二次函数的各种性质是解题关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
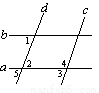
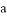 ∥
∥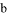 B. ∵∠1=∠2,∴
B. ∵∠1=∠2,∴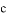 ∥
∥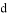 D. ∵∠1=∠3,∴
D. ∵∠1=∠3,∴ 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
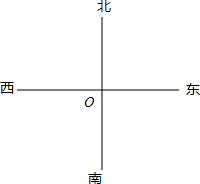 甲、乙两船同时从小岛O出发,甲船速度为40海里/时,沿北偏西20°的方向航行;乙船沿北偏东70°的方向,以30海里/时的速度航行,半小时后甲、乙两船分别到达A,B两处.
甲、乙两船同时从小岛O出发,甲船速度为40海里/时,沿北偏西20°的方向航行;乙船沿北偏东70°的方向,以30海里/时的速度航行,半小时后甲、乙两船分别到达A,B两处.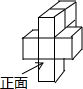 如果用□表示1个立方体,用
如果用□表示1个立方体,用 表示两个立方体叠加,用■表示三个立方体叠加,那么下面图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )
表示两个立方体叠加,用■表示三个立方体叠加,那么下面图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )