题目内容
1.若x2-4x+m=(x-2)(x+n),则m=4,n=-2.分析 直接利用多项式乘法运算法则进而得出m,n的值即可.
解答 解:∵x2-4x+m=(x-2)(x+n),
∴x2-4x+m=x2+(n-2)x-2n,
故n-2=-4,m=-2n,
解得:n=-2,m=4.
故答案为:4,-2.
点评 此题主要考查了多项式乘法以及十字相乘应用,正确利用运算法则是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知a=$\sqrt{2}$,b=$\sqrt{5}$,则$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}÷\frac{1}{a}$的值为( )
| A. | $\sqrt{5}-\sqrt{2}$ | B. | 3 | C. | $\sqrt{2}+\sqrt{5}$ | D. | $\sqrt{2}-\sqrt{5}$ |
15.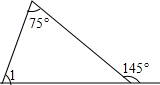 如图,∠1的度数是( )
如图,∠1的度数是( )
 如图,∠1的度数是( )
如图,∠1的度数是( )| A. | 75° | B. | 60° | C. | 85° | D. | 70° |
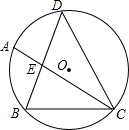 如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E,
如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E,