题目内容
19. 如图,等腰三角形ABC内接于半径为5的⊙O,AB=AC,tan∠ABC=$\frac{1}{3}$.求BC的长.
如图,等腰三角形ABC内接于半径为5的⊙O,AB=AC,tan∠ABC=$\frac{1}{3}$.求BC的长.
分析 连接AO,交BC于点E,连接BO,证出$\widehat{AB}=\widehat{AC}$,根据垂径定理得出OA⊥BC,BC=2BE,设AE=x,则BE=3x,OE=5-x,根据勾股定理得出方程(3x)2+(5-x)2=52,求出方程的解,即可得出答案.
解答 解:连接OA,OB,如图所示: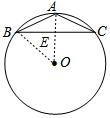
∵AB=AC,
∴$\widehat{AB}=\widehat{AC}$,
∴OA垂直平分BC于点H,
∴OA⊥BC,BC=2BE,
在Rt△ABE中,∵tan∠ABC=$\frac{1}{3}$,
∴$\frac{AE}{BE}$=$\frac{1}{3}$,
设AE=x,则BE=3x,OE=5-x,
在Rt△EO中,BE2+OE2=OB2,
∴(3x)2+(5-x)2=52,
解得:x1=0(舍去),x2=1,
∴BE=3x=3,
∴BC=2BE=6.
点评 本题考查了圆心角、弧、弦之间的关系,垂径定理,解直角三角形,勾股定理的应用,解此题的关键是构造直角三角形,用了方程思想,难度适中.

练习册系列答案
相关题目
9.“$\frac{4}{9}$的平方根是$±\frac{2}{3}$”,用式子表示就是( )
| A. | $±\sqrt{\frac{4}{9}}=\frac{2}{3}$ | B. | $±\sqrt{\frac{4}{9}}=±\frac{2}{3}$ | C. | $\sqrt{\frac{4}{9}}=\frac{2}{3}$ | D. | $\sqrt{\frac{4}{9}}=±\frac{2}{3}$ |
4. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )| A. | ∠A=∠1+∠2 | B. | 3∠A=2∠1+∠2 | C. | 2∠A=∠1+∠2 | D. | 3∠A=2(∠1+∠2) |
11.如果a<b,那么下列不等式中一定成立的是( )
| A. | a2<ab | B. | ab<b2 | C. | a2<b2 | D. | a-2b<-b |
 甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是87.5米.
甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是87.5米.