题目内容
13.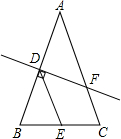 如图,在△ABC中,AB=AC,点D、F分别在AB,AC上,DF垂直平分AB,E是BC的中点,若∠C=70°,则∠EDF=50°.
如图,在△ABC中,AB=AC,点D、F分别在AB,AC上,DF垂直平分AB,E是BC的中点,若∠C=70°,则∠EDF=50°.
分析 根据线段垂直平分线的性质,可得∠BDF度数,根据等腰三角形的性质,可得∠B的度数,根据三角形中位线的性质,可得∠DEB的度数,根据三角形内角和定理,可得∠BDE的度数,根据余角的定义,可得答案.
解答 解:由DF垂直平分AB,得
∠BDF=90°,AD=BD.
又由E是BC的中点,得
DE∥AC,
∠DEB=∠C=70°.
由AB=AC,得
∠B=∠C=70°.
由三角形的内角和定理,得
∠BDE=180°-∠B-∠DEB=180°-70°-70°=40°.
由余角的定义,得
∠EDF=∠BDF-∠BDE=90°-40°=50°,
故答案为:50°.
点评 本题考查了线段垂直平分线的性质,利用了线段的垂直平分线,三角形中位线定理,等腰三角形的性质,三角形内角和定理,余角的定义,考查知识点较多,稍有难度.

练习册系列答案
相关题目
3.为了估计县城空气质量情况,某同学在30天里做了如下记录:
其中w<50时空气质量为优,50≤w≤100时空气质量为良,100<w≤150时空气质量为轻度污染,若1年按365天计算,请你估计该城市在一年中空气质量达到良以上(含良)的天数为292 天.
| 污染指数(w) | 40 | 60 | 80 | 100 | 120 | 140 |
| 天数(天) | 2 | 6 | 9 | 7 | 5 | 1 |
8.计算a2÷a3的结果是( )
| A. | a-1 | B. | a | C. | a5 | D. | a6 |