题目内容
11. 已知数轴甲上有A、B、C三点,分别表示-30、-20、0,动点M从点A出发,以每秒1个单位的速度向终点C移动,设点M移动的时间为t秒,点M在数轴甲上表示的数为m.
已知数轴甲上有A、B、C三点,分别表示-30、-20、0,动点M从点A出发,以每秒1个单位的速度向终点C移动,设点M移动的时间为t秒,点M在数轴甲上表示的数为m.(1)用含有t的代数式表示m=t-30(0≤t≤30).
(2)另有一个数轴乙,数轴乙上有D、E两点,分别表示-60、0.当点M运动到点B时,数轴乙上的动点N从点D出发,以点M速度的4倍向点E运动,当N到达点E后,再立即以同样的速度返回,当点M到达点C时,M、N两点运动停止,设点N在数轴乙上表示数n.
①当点N从点D出发,向点E运动时,用含有t的代数式表示n=4t-100(10≤t≤25);当点N到达点E后返回时,用含有t的代数式表示n=100-4t(25<t).
②求当点N从开始运动到运动停止时,m-n的值(用含t的代数式表示)
③求当t为何值时,m=n.
分析 (1)根据“点M表示的数=点A表示的数+点M运动的速度×运动时间”即可得出n的值;
(2)①分别找出运动的时间,再根据数量关系即可找出n的值;②按时间分段求m-n即可;③按时间分段,根据m=n找出关于t的一元一次方程,解方程即可得出结论.
解答 解:(1)由已知得:m=-30+t=t-30(0≤t≤30).
故答案为:t-30(0≤t≤30).
(2)①M点从点A运动到点B所需时间为:[-20-(-30)]÷1=10(秒),
∴点N运动的时间为:t-10,
∴当点N从点D出发,向点E运动时:n=-60+4(t-10)=4t-100(10≤t≤25);
N点从点D运动到点E所需时间为:[0-(-60)]÷4=15(秒),
∴点N从点E返回运动的时间为:t-10-15=t-25,
∴当点N到达点E后返回时:n=-4(t-25)=100-4t(25<t).
故答案为:4t-100(10≤t≤25);100-4t(25<t).
②当10≤t≤25时,m-n=t-30-(4t-100)=70-3t;
当25<t时,m-n=t-30-(100-4t)=5t-130.
∴m-n=$\left\{\begin{array}{l}{70-3t(10≤t≤25)}\\{5t-130(t>25)}\end{array}\right.$.
③当10≤t≤25时,m=n,即t-30=4t-100,
解得:t=$\frac{70}{3}$;
当25<t时,m=n,即t-30=100-4t,
解得:t=26.
故当t为$\frac{70}{3}$或26秒时,m=n.
点评 本题考查了一元一次方程的应用以及数轴,解题的关键是:(1)根据数量关系表示出来m;(2)根据数量关系表示出n.本题属于基础题,难度不大,解决该题型题目时,根据时间t的范围分段是关键.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | ±2 | B. | -2 | C. | 2 | D. | $±\frac{1}{2}$ |
| A. | 3,7,8 | B. | 4,5,6 | C. | 6,8,15 | D. | 8,9,15 |
| A. | 正比例函数 | B. | 反比例函数 | ||
| C. | 图象不经过原点的一次函数 | D. | 二次函数 |
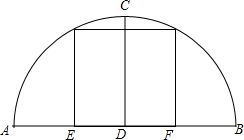 如图为一圆弧形拱桥,桥下水面宽为AB=24米,拱顶高出水面CD=8米.现有一艘宽EF=8米,且船舱顶部为矩形的货船要经过这里,那么货船高出水面的部分最多不能超过多少米?
如图为一圆弧形拱桥,桥下水面宽为AB=24米,拱顶高出水面CD=8米.现有一艘宽EF=8米,且船舱顶部为矩形的货船要经过这里,那么货船高出水面的部分最多不能超过多少米?