题目内容
6.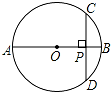 如图,AB是⊙O的直径,弦CD⊥AB,CD=10,AP:PB=5:1,⊙O的半径是( )
如图,AB是⊙O的直径,弦CD⊥AB,CD=10,AP:PB=5:1,⊙O的半径是( )| A. | 6 | B. | $5\sqrt{5}$ | C. | 8 | D. | $3\sqrt{5}$ |
分析 连接OC,根据AP:PB=5:1可设PB=x,AP=5x,故OC=OB=$\frac{5x+x}{2}$=3x,故OP=2x,由垂径定理可求出PC的长,根据勾股定理求出x的值,进而可得出结论.
解答 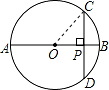 解:连接OC,
解:连接OC,
∵AP:PB=5:1,
∴设PB=x,AP=5x,
∴OC=OB=$\frac{5x+x}{2}$=3x,
∴OP=2x.
∵AB是⊙O的直径,弦CD⊥AB,CD=10,
∴PC=5.
∵PC2+OP2=OC2,即52+(2x)2=(3x)2,解得x=$\sqrt{5}$,
∴OC=3x=3$\sqrt{5}$.
故选D.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知反比例函数y=$\frac{10}{x}$,当1<x<2时,y的取值范围是( )
| A. | 0<x<5 | B. | 1<y<2 | C. | 5<y<10 | D. | y>10 |
 如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,则∠DAE=15度.
如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,则∠DAE=15度. 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地.设原正方形空地的边长为xm,则根据题意所列方程是(x-3)(x-2)=20.
如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地.设原正方形空地的边长为xm,则根据题意所列方程是(x-3)(x-2)=20.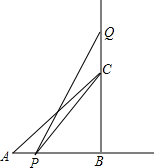 如图,在△ABC中,∠B=90°,AB=BC=10cm,点P从点A出发沿射线AB以1cm/s的速度作直线运动,点Q从点C出发沿射线BC以2cm/s的速度作直线运动.如果P,Q分别从A,B同时出发,经过几秒,S△PCQ=$\frac{12}{25}$S△ABC?
如图,在△ABC中,∠B=90°,AB=BC=10cm,点P从点A出发沿射线AB以1cm/s的速度作直线运动,点Q从点C出发沿射线BC以2cm/s的速度作直线运动.如果P,Q分别从A,B同时出发,经过几秒,S△PCQ=$\frac{12}{25}$S△ABC? 如图,在等腰△ABC中,AB=AC,分别作CD⊥AB,BE⊥AC,EG⊥AB,DF⊥AC.求证:四边形MDNE是菱形.
如图,在等腰△ABC中,AB=AC,分别作CD⊥AB,BE⊥AC,EG⊥AB,DF⊥AC.求证:四边形MDNE是菱形.