题目内容
18.如图,双曲线y=$\frac{k}{x}$经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=-$\frac{18}{x}$于点C,直线y=m(m≠0)分别交双曲线y=-$\frac{18}{x}$、y=$\frac{k}{x}$于点P、Q.(1)求k的值;
(2)若△OAP为直角三角形,求点P的坐标;
(3)△OCQ的面积记为S△OCQ,△OAP的面积记为S△OAP,试比较S△OCQ与S△OAP的大小(直接写出结论).
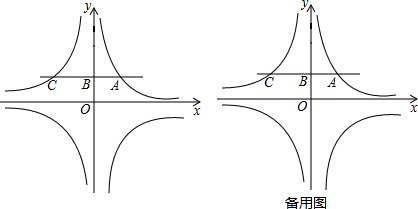
分析 (1)直接把点A(1,2)代入双曲线y=$\frac{k}{x}$,求出k的值即可;
(2)设P(-$\frac{18}{m}$,m),再分∠AOP=90°,∠OAP=90°及∠APO=90°三种情况进行讨论;
(3)根据A(1,2)可得出C(-9,2),设P(-$\frac{18}{m}$,m),则Q($\frac{2}{m}$,m),分别过点A、Q、P、C作x轴的垂线,垂足分别为M、N、K、H,再由反比例函数图象上点的坐标特点得出△AOM,△QON,△COH与△POK的面积,根据S△OCQ=S梯形CHNQ-S△COH-S△POK,S△OAP=S梯形AMKP-S△AOM-S△POK即可得出结论.
解答 解:(1)∵双曲线y=$\frac{k}{x}$经过点A(1,2),
∴k=1×2=2;
(2)设P(-$\frac{18}{m}$,m),
∵A(1,2),
∴OA2=12+22=5,AP2=(1+$\frac{18}{m}$)2+(2-m)2,OP2=($\frac{18}{m}$)2+m2,
当∠AOP=90°时,
∵OA2+OP2=AP2,即5+($\frac{18}{m}$)2+m2=(1+$\frac{18}{m}$)2+(2-m)2,解得m=±3,
∴P1(-6,3),P2(6,-3);
当∠OAP=90°时,
∵OA2+AP2=OP2,即5+(1+$\frac{18}{m}$)2+(2-m)2=($\frac{18}{m}$)2+m2,解得m=$\frac{9±3\sqrt{73}}{8}$,
∴P3($\frac{9-3\sqrt{73}}{4}$,$\frac{9+3\sqrt{73}}{8}$),P4($\frac{9+3\sqrt{73}}{4}$,$\frac{9-3\sqrt{73}}{8}$);
当∠APO=90°时,此种情况不存在;
(3)∵A(1,2),
∴C(-9,2).
设P(-$\frac{18}{m}$,m),则Q($\frac{2}{m}$,m),
分别过点A、Q、P、C作x轴的垂线,垂足分别为M、N、K、H,
∵点A、Q在反比例函数y=$\frac{2}{x}$的图象上,
∴S△AOM=S△QON=1.
∵点C、P在反比例函数y=-$\frac{18}{x}$的图象上,
∴S△COH=S△POK=9.
S△OCQ=S梯形CHNQ-S△COH-S△POK,S△OAP=S梯形AMKP-S△AOM-S△POK,
∴S△OCQ-S△OAP=S梯形CHNQ-S梯形AMKP,
∵梯形CHNQ与梯形AMKP的上底与下底相同,
∴只要比较HN与KM的大小即可,
∵HN-KM=(9+$\frac{2}{\left|m\right|}$)-(1+$\frac{18}{\left|m\right|}$)=8-$\frac{16}{\left|m\right|}$,
∴当m=±2时,HN=KM,即S△OCQ=S△OAP;
当m>2或m<-2时,8-$\frac{16}{\left|m\right|}$>0,即S△OCQ>S△OAP;
当-2<m<2时,8-$\frac{16}{\left|m\right|}$<0,即S△OCQ<S△OAP.
点评 本题考查的是反比例函数综合题,在解答此题时要注意进行分类讨论,不要漏解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{6}$ |
 为加强我县创建文明卫生县城宣传力度,需要在甲楼A处到E处悬挂一幅宣传条幅,在乙楼顶部D点测得条幅顶端A点的仰角为45°,条幅底端E点的仰角为30°,若甲、乙两楼的水平距离BC为21米,求条幅的长约是多少米?(结果精确到0.1米).
为加强我县创建文明卫生县城宣传力度,需要在甲楼A处到E处悬挂一幅宣传条幅,在乙楼顶部D点测得条幅顶端A点的仰角为45°,条幅底端E点的仰角为30°,若甲、乙两楼的水平距离BC为21米,求条幅的长约是多少米?(结果精确到0.1米).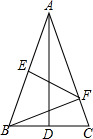 如图,△ABC,AB=AC,AD为△ABC的角平分线,过AB的中点E作AB的垂线交AC于点F,连接BF,若AB=5,CD=2,则△BFC的周长为( )
如图,△ABC,AB=AC,AD为△ABC的角平分线,过AB的中点E作AB的垂线交AC于点F,连接BF,若AB=5,CD=2,则△BFC的周长为( )