题目内容
 如图,PC经过圆心O,弦AB⊥PC于点D.连接BC和PA,且∠PAB=2∠PCB.
如图,PC经过圆心O,弦AB⊥PC于点D.连接BC和PA,且∠PAB=2∠PCB.(1)求证:PA为圆O的切线;
(2)延长PA至点E,使PE=PC,若tan∠PCB=
| 1 |
| 3 |
考点:切线的判定
专题:证明题
分析:(1)连接AO,CF为直径,如图,根据垂径定理得弧AF=弧BF,再根据圆周角定理得到∠AOF=2∠PCB,由于∠PAB=2∠PCB,则∠PAB=∠AOP,而∠AOD+∠DAO=90°,于是∠PAD+∠DAO=90°,然后根据切线的判定定理可得PA为圆O的切线;
(2)作EH⊥PC于H,连接AF,如图,在Rt△BDC中,利用正切的定义得tan∠DCB=
=
,于是可设BD=x,则CD=3x,由垂径定理得到AD=BD=x,由圆周角定理得到∠FAD=∠FCB,则在Rt△AFD中,tan∠FAD=
=
,则FD=
x,FC=FD+CD=
x;接着在Rt△APD中,根据勾股定理得PA2=PD2+AD2=PD2+x2,
加上由切割线定理得PA2=PF•PC=(PD-FD)•(PD+CD)=(PD-
x)(PD+3x),所以PD2+x2=(PD-
x)(PD+3x),解得PD=
x,易得PA=
x,PC=
x,由PE=PC=
x得∠PEC=∠PCB,然后证明△PAD∽△PEH,利用相似比可得EH=
x,PH=
x,则CH=PC-PH=
x,在Rt△EHC中利用勾股定理计算出EC=
x,则根据正弦的定义得sin∠ECH=
=
,所以sin∠PEC=
.
(2)作EH⊥PC于H,连接AF,如图,在Rt△BDC中,利用正切的定义得tan∠DCB=
| BD |
| CD |
| 1 |
| 3 |
| FD |
| AD |
| 1 |
| 3 |
| 1 |
| 3 |
| 10 |
| 3 |
加上由切割线定理得PA2=PF•PC=(PD-FD)•(PD+CD)=(PD-
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
| 13 |
| 3 |
| 13 |
| 3 |
| 13 |
| 5 |
| 52 |
| 15 |
| 13 |
| 15 |
13
| ||
| 15 |
| EH |
| EC |
3
| ||
| 10 |
3
| ||
| 10 |
解答:(1)证明:连接AO,CF为直径,如图,
∵弦AB⊥PC于点D,
∴弧AF=弧BF,∠AOD=90°,
∴∠AOF=2∠PCB,
∵∠PAB=2∠PCB,
∴∠PAB=∠AOP,
∵∠AOD+∠DAO=90°,
∴∠PAD+∠DAO=90°,即∠PAO=90°,
∴OA⊥PA,
∴PA为圆O的切线;
(2)解:作EH⊥PC于H,连接AF,如图,
在Rt△BDC中,tan∠DCB=
=
,
设BD=x,则CD=3x,
∵AB⊥CF,
∴AD=BD=x,
∵∠FAD=∠FCB,
∴在Rt△AFD中,tan∠FAD=
=
,
∴FD=
x,
∴FC=FD+CD=
x+3x=
x,
在Rt△APD中,PA2=PD2+AD2=PD2+x2,
∵PA为圆O的切线,
∴PA2=PF•PC=(PD-FD)•(PD+CD)=(PD-
x)(PD+3x),
∴PD2+x2=(PD-
x)(PD+3x),解得PD=
x,
∴PA2=PD2+x2=(
x)2+x2=
x2,解得PA=
x,
PC=PD+CD=
x,
∵PE=PC,
∴PE=
x,∠PEC=∠PCB,
∵AD∥EH,
∴△PAD∽△PEH,
∴
=
=
,即
=
=
,解得EH=
x,PH=
x,
∴CH=PC-PH=
x-
x=
x,
在Rt△EHC中,EC=
=
x,
∴sin∠ECH=
=
=
,
∴sin∠PEC=
.
∵弦AB⊥PC于点D,
∴弧AF=弧BF,∠AOD=90°,
∴∠AOF=2∠PCB,
∵∠PAB=2∠PCB,
∴∠PAB=∠AOP,
∵∠AOD+∠DAO=90°,
∴∠PAD+∠DAO=90°,即∠PAO=90°,
∴OA⊥PA,

∴PA为圆O的切线;
(2)解:作EH⊥PC于H,连接AF,如图,
在Rt△BDC中,tan∠DCB=
| BD |
| CD |
| 1 |
| 3 |
设BD=x,则CD=3x,
∵AB⊥CF,
∴AD=BD=x,
∵∠FAD=∠FCB,
∴在Rt△AFD中,tan∠FAD=
| FD |
| AD |
| 1 |
| 3 |
∴FD=
| 1 |
| 3 |
∴FC=FD+CD=
| 1 |
| 3 |
| 10 |
| 3 |
在Rt△APD中,PA2=PD2+AD2=PD2+x2,
∵PA为圆O的切线,
∴PA2=PF•PC=(PD-FD)•(PD+CD)=(PD-
| 1 |
| 3 |
∴PD2+x2=(PD-
| 1 |
| 3 |
| 4 |
| 3 |
∴PA2=PD2+x2=(
| 4 |
| 3 |
| 25 |
| 9 |
| 5 |
| 3 |
PC=PD+CD=
| 13 |
| 3 |
∵PE=PC,
∴PE=
| 13 |
| 3 |
∵AD∥EH,
∴△PAD∽△PEH,
∴
| AD |
| EH |
| PD |
| PH |
| PA |
| PE |
| x |
| EH |
| ||
| PH |
| ||
|
| 13 |
| 5 |
| 52 |
| 15 |
∴CH=PC-PH=
| 13 |
| 3 |
| 52 |
| 15 |
| 13 |
| 15 |
在Rt△EHC中,EC=
| EH2+CH2 |
13
| ||
| 15 |
∴sin∠ECH=
| EH |
| EC |
| ||||
|
3
| ||
| 10 |
∴sin∠PEC=
3
| ||
| 10 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了切割线定理、勾股定理、相似三角形的判定与性质以及锐角三角函数的定义.

练习册系列答案
相关题目
 如图所示的6个数是按一定规律排列的,根据这个规律,括号内的数应是( )
如图所示的6个数是按一定规律排列的,根据这个规律,括号内的数应是( )| A、27 | B、56 | C、43 | D、30 |
 如图,在此图中小于平角的角有( )个.
如图,在此图中小于平角的角有( )个.| A、8 | B、9 | C、10 | D、11 |
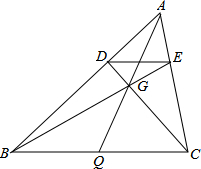 在△ABC中,作DE∥BC,连BE、CD交于一点G,连AG延长至BC上于Q.证明:Q是BC中点.
在△ABC中,作DE∥BC,连BE、CD交于一点G,连AG延长至BC上于Q.证明:Q是BC中点. 如图:已知AD∥BC,AD=CB,A、E、F、C在同一直线上且AE=CF,
如图:已知AD∥BC,AD=CB,A、E、F、C在同一直线上且AE=CF,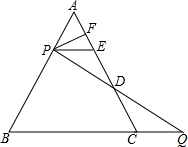 如图,△ABC是等边三角形,P是AB上一点,Q是BC延长线上一点,AP=CQ.联结PQ交AC于D点.过P作PE∥BC,交AC于E点.
如图,△ABC是等边三角形,P是AB上一点,Q是BC延长线上一点,AP=CQ.联结PQ交AC于D点.过P作PE∥BC,交AC于E点.