题目内容
8．在平行四边形ABCD中，∠B=30°，AB=12cm，AD=14cm，则平行四边形ABCD的面积为（ ）| A． | 21cm2 | B． | 42cm2 | C． | 168cm2 | D． | 84cm2 |
分析 直接利用直角三角形的性质得出平行四边形的高，再根据平行四边形的面积等于它的底和这个底上的高的积进而求出其面积．
解答 解：
作AE⊥BC于E，如图所示：
∵在?ABCD中，AB=12cm，AD=14cm，
∴CB=14cm，
∵∠B=30°，
∴AE=$\frac{1}{2}$AB=6cm，
∴?ABCD的面积为：14×6=84cm2；
故选：D．
点评 此题主要考查了平行四边形的性质、直角三角形的性质，正确得出平行四边形的高是解题关键．
练习册系列答案
相关题目
13．抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：
从上表可知，下列说法中正确的是（ ）
①抛物线与x轴的一个交点为（3，0）；
②函数y=ax2+bx+c的最大值为6；
③抛物线的对称轴是直线x=$\frac{1}{2}$；
④在对称轴左侧，y随x增大而增大．
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与x轴的一个交点为（3，0）；
②函数y=ax2+bx+c的最大值为6；
③抛物线的对称轴是直线x=$\frac{1}{2}$；
④在对称轴左侧，y随x增大而增大．
| A． | ①②③ | B． | ①③④ | C． | ①②④ | D． | ②③④ |
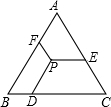如图，P是等边三角形ABC内任一点，过点P作PD∥AB，PE∥BC，PF∥AC，分别交BC、AC、AB于点D、E、F．求证：PD+PE+PF=BC．
如图，已知AB、CD是⊙O的弦，AB⊥CD，垂足为点E，AB被CD分成3厘米、14厘米两段（AE＜EB），求点O到CD的距离．