题目内容
18．在下列直线中，与直线y=x+3相交于第二象限的是（ ）| A． | y=x | B． | y=2x | C． | y=kx+2k+1（k≠1） | D． | y=kx-2k+1（k≠0） |
分析 利用两直线平行的问题可对A进行判断；利用直线y=2x不经过第二象限可对B进行判断；利用直线y=kx+2k+1（k≠1）过定点（-2，1）可对C进行判断；利用k=1时，直线y=kx-2k+1与直线y=x+3平行可对D进行判断．
解答 解：A、直线y=x与直线y=x+3平行，它们没有交点，所以A选项错误；
B、直线y=2x经过第一、三象限，所以B选项错误；
C、直线y=kx+2k+1（k≠1）一定过定点（-2，1），而点（-2，1）在直线y=x+3上，所以C选项正确；
D、直线y=kx-2k+1（k≠0）一定过定点（2，1），而点（2，1）在第一象限，且当k=1时，直线y=kx-2k+1与直线y=x+3平行，所以D选项错误．
故选C．
点评 本题考查了两直线相交或平行问题：两条直线的交点坐标，就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解．若两条直线是平行的关系，那么他们的自变量系数相同，即k值相同．对C进行判断的关键是确定该直线过定点．
练习册系列答案
相关题目
13．
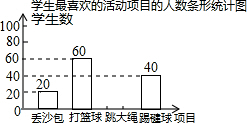我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动，为了解学生对四种项目的喜欢情况，随机调查了该校m名学生最喜欢的一种项目（每名学生必选且只能选择四种活动项目的一种），并将调查结果绘制成如下的不完整的统计图表：
学生最喜欢的活动项目的人数统计表
根据图表中提供的信息，解答下列问题：
（1）m=200，n=80，p=30；
（2）请根据以上信息直接补全条形统计图；
（3）根据抽样调查结果，请你估计该校2000名学生中有多少名学生最喜欢跳大绳．
我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动，为了解学生对四种项目的喜欢情况，随机调查了该校m名学生最喜欢的一种项目（每名学生必选且只能选择四种活动项目的一种），并将调查结果绘制成如下的不完整的统计图表：学生最喜欢的活动项目的人数统计表
| 项目 | 学生数（名） | 百分比 |
| 丢沙包 | 20 | 10% |
| 打篮球 | 60 | p% |
| 跳大绳 | n | 40% |
| 踢毽球 | 40 | 20% |
（1）m=200，n=80，p=30；
（2）请根据以上信息直接补全条形统计图；
（3）根据抽样调查结果，请你估计该校2000名学生中有多少名学生最喜欢跳大绳．
3．
如图，平行四边形ABCD的对角线AC、BD交于点O，若AC=DC=4，BD=6，则△AOB的周长为（ ）
如图，平行四边形ABCD的对角线AC、BD交于点O，若AC=DC=4，BD=6，则△AOB的周长为（ ）| A． | 14 | B． | 12 | C． | 10 | D． | 9 |
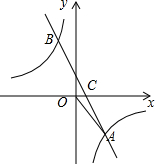如图，已知点A（3，m），B（-2，6）在反比例函数$y=\frac{k}{x}$的图象上，直线AB与x轴交于点C．
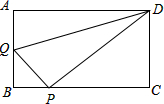在矩形ABCD中，AB=3，AD=4，动点Q从点A出发，以每秒1个单位的速度，沿AB向点B移动；同时点P从点B出发，仍以每秒1个单位的速度，沿BC向点C移动，连接QP，QD，PD．若两个点同时运动的时间为x秒（0＜x≤3），解答下列问题：