��Ŀ����
13��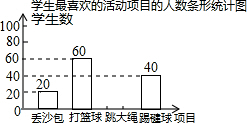 ����ij��ѧ������ѧ���п�չ��ɳ�����������������������������Ŀ�Ļ��Ϊ�˽�ѧ����������Ŀ��ϲ���������������˸�Уm��ѧ����ϲ����һ����Ŀ��ÿ��ѧ����ѡ��ֻ��ѡ�����ֻ��Ŀ��һ�֣����������������Ƴ����µIJ�������ͳ��ͼ����
����ij��ѧ������ѧ���п�չ��ɳ�����������������������������Ŀ�Ļ��Ϊ�˽�ѧ����������Ŀ��ϲ���������������˸�Уm��ѧ����ϲ����һ����Ŀ��ÿ��ѧ����ѡ��ֻ��ѡ�����ֻ��Ŀ��һ�֣����������������Ƴ����µIJ�������ͳ��ͼ����ѧ����ϲ���Ļ��Ŀ������ͳ�Ʊ�
| ��Ŀ | ѧ���������� | �ٷֱ� |
| ��ɳ�� | 20 | 10% |
| ������ | 60 | p% |
| ������ | n | 40% |
| ����� | 40 | 20% |
��1��m=200��n=80��p=30��
��2�������������Ϣֱ�Ӳ�ȫ����ͳ��ͼ��
��3�����ݳ�����������������Ƹ�У2000��ѧ�����ж�����ѧ����ϲ����������
���� ��1������20��10%=200�����ɵõ�m��ֵ����200��40%���ɵõ�n��ֵ����60��200���ɵõ�p��ֵ��
��2������n��ֵ���ɲ�ȫ����ͳ��ͼ��
��3�������������������壬2000��40%�����ɽ��
��� �⣺��1��m=20��10%=200��n=200��40%=80��60��200=30%��p=30��
�ʴ�Ϊ��200��80��30��
��2����ͼ��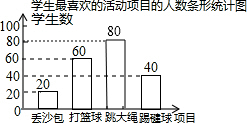
��3��2000��40%=800���ˣ���
�𣺹��Ƹ�У2000��ѧ������800��ѧ����ϲ����������
���� ���⿼��������ͳ��ͼ������ͳ��ͼ�����ʹ�ʽ������ͳ��ͼ����ͳ��ͼ�еõ���Ҫ����Ϣ�ǽ������Ĺؼ�������ͳ��ͼ������ر�ʾ��ÿ����Ŀ�����ݣ�

��ϰ��ϵ�д�
 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
�����Ŀ
1��������������������ǣ�������
| A�� | ͬλ����� | |
| B�� | �����ε������ڽ��У�������һ��������60�� | |
| C�� | �κ���������ݶ���1 | |
| D�� | ��ֱ��ͬһֱ�ߵ�����ֱ���ഹֱ |
18��������ֱ���У���ֱ��y=x+3�ཻ�ڵڶ������ǣ�������
| A�� | y=x | B�� | y=2x | C�� | y=kx+2k+1��k��1�� | D�� | y=kx-2k+1��k��0�� |
5�����ı��ʽ��ֵ��ʹ��ʽ$\frac{{\frac{1}{2}{x^2}+\frac{1}{3}}}{{\frac{1}{2}{x^2}-\frac{1}{3}{x^3}}}$�ķ��Ӻͷ�ĸ�����ϵ��������������Ľ��Ϊ��������
| A�� | $\frac{{2{x^2}+3}}{{2{x^2}-3{x^3}}}$ | B�� | $\frac{{3{x^2}+2}}{{2{x^2}-3{x^3}}}$ | C�� | $\frac{{3{x^2}+2}}{{3{x^2}-2{x^3}}}$ | D�� | $\frac{{3{x^2}+2}}{{3{x^3}-2{x^2}}}$ |
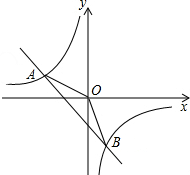 ��ͼ��ʾ��һ�κ���y1=kx+b��ͼ���뷴��������y2=$\frac{m}{x}$��ͼ����A��-2��n����B��1��-3�����㣮
��ͼ��ʾ��һ�κ���y1=kx+b��ͼ���뷴��������y2=$\frac{m}{x}$��ͼ����A��-2��n����B��1��-3�����㣮 ��ֱ֪��y=kx+b��x�ᡢy��ֱ���A��B���㣬�뷴������������һ�����ڵ�P��$\frac{1}{2}$��n����Q��4��m�����㣬��tan��BOP=$\frac{1}{16}$��
��ֱ֪��y=kx+b��x�ᡢy��ֱ���A��B���㣬�뷴������������һ�����ڵ�P��$\frac{1}{2}$��n����Q��4��m�����㣬��tan��BOP=$\frac{1}{16}$��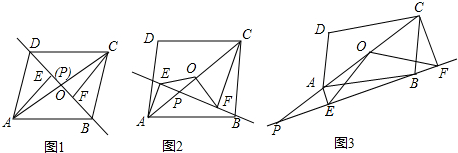
 ʵ��a�������ϵ�λ����ͼ����|a-3|=3-a��
ʵ��a�������ϵ�λ����ͼ����|a-3|=3-a�� ��֪�߶�AB=14cm��CΪ�߶�AB����һ�㣬D��AC���е㣬E��CB���е㣬��DE�ij��ȣ�
��֪�߶�AB=14cm��CΪ�߶�AB����һ�㣬D��AC���е㣬E��CB���е㣬��DE�ij��ȣ�