题目内容
1．若抛物线y=2x2-（m+3）x-m+7的对称轴是x=1，则m=1．分析 抛物线y=ax2+bx+c的对称轴为直线x=-$\frac{b}{2a}$，根据对称轴公式可求m的值．
解答 解：∵抛物线y=2x2-（m+3）x-m+7，
∴对称轴x=-$\frac{b}{2a}$=$\frac{-（m+3）}{4}$=1，
解得：m=1．
故答案为：1．
点评 本题考查了二次函数的性质，熟记对称轴公式是解题的关键．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
如图，正方形ABCD与正方形CEFG（边长不等），B、C、F三点共线，连接BE交CD于M，连接DG交BE、CE、CF分别于N、P、Q，以下四个结论：①BE=DG；②BM=DQ；③CM=CP；④∠BNQ=90°恒成立的有①②④（把你认为正确的序号都填上）．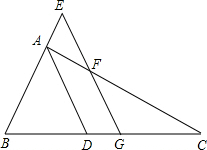
如图，AD为△ABC的角平分线，G为BC中点，GE∥AD，分别交BA的延长线于E，交AC于F，求证：
13．在-6，7，8，-$\frac{1}{9}$，12，0，-0.33，$\frac{2}{5}$各数中，负分数的个数有（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |