题目内容
14.若x+y=-8,xy=12,则y$\sqrt{\frac{y}{x}}$+x$\sqrt{\frac{x}{y}}$的值是$\frac{20\sqrt{3}}{3}$.分析 根据分式加减运算法则,将所求代数式转化为$\frac{{y}^{2}+{x}^{2}}{\sqrt{x}•\sqrt{y}}$,然后将x2+y2转化为(x+y)2-2xy就可解决问题.
解答 解:当x+y=-8,xy=12时,
y$\sqrt{\frac{y}{x}}$+x$\sqrt{\frac{x}{y}}$=$\frac{y\sqrt{y}}{\sqrt{x}}$+$\frac{x\sqrt{x}}{\sqrt{y}}$=$\frac{{y}^{2}+{x}^{2}}{\sqrt{x}•\sqrt{y}}$=$\frac{(x+y)^{2}-2xy}{\sqrt{xy}}$=$\frac{64-24}{\sqrt{12}}$=$\frac{40}{2\sqrt{3}}$=$\frac{20\sqrt{3}}{3}$.
点评 本题主要考查了分式加减运算法则、完全平方公式等知识,在四个量x+y、x-y、xy、x2+y2中,若知道两个量,就可根据完全平方公式求出其它的两个量.

练习册系列答案
相关题目
9.两个连续的正偶数的积为360,则这两个正偶数为( )
| A. | -18,-16或18,20 | B. | 18,20 | C. | 18 | D. | 20 |
3.实数-2的相反数是( )
| A. | 2 | B. | -2 | C. | 0.5 | D. | -0.5 |
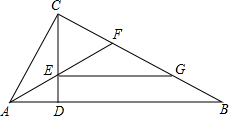 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D点,AF平分∠BAC交CD于E点,交BC于F点,EG∥AB交BC于G点.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D点,AF平分∠BAC交CD于E点,交BC于F点,EG∥AB交BC于G点. 根据图回答下列问题:
根据图回答下列问题: