题目内容
已知在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为(1,1)和(4,0),如果将△OAB绕着原点O旋转后,点A落在x轴上,点B落在点C处,那么cot∠OCB的值为 .
考点:坐标与图形变化-旋转
专题:
分析:根据点A的坐标判断出OA与x轴的夹角为45°,再根据旋转的性质可得OB=OC,根据等边对等角可得∠OCB=∠OBC,过点C作CD⊥x轴于D,然后求出OD、CD,再分两种情况求出BD,然后根据余切的定义列式计算即可得解.
解答: 解:∵A(1,1),
解:∵A(1,1),
∴OA与x轴的夹角为45°,
∴旋转后OB与x轴的夹角为45°且OB=OC,
∴∠OCB=∠OBC,
过点C作CD⊥x轴于D,
则OD=CD=
OB=
×4=2
,
如图,若顺时针旋转,则BD=OB-OD=4-2
,
cot∠OCB=
=
=
-1,
若逆时针旋转,则BD=OB+OD=4+2
,
cot∠OCB=
=
=
+1,
综上所述,cot∠OCB的值为
+1或
-1.
故答案为:
+1或
-1.
 解:∵A(1,1),
解:∵A(1,1),∴OA与x轴的夹角为45°,
∴旋转后OB与x轴的夹角为45°且OB=OC,
∴∠OCB=∠OBC,
过点C作CD⊥x轴于D,
则OD=CD=
| ||
| 2 |
| ||
| 2 |
| 2 |
如图,若顺时针旋转,则BD=OB-OD=4-2
| 2 |
cot∠OCB=
| BD |
| CD |
4-2
| ||
2
|
| 2 |
若逆时针旋转,则BD=OB+OD=4+2
| 2 |
cot∠OCB=
| BD |
| CD |
4+2
| ||
2
|
| 2 |
综上所述,cot∠OCB的值为
| 2 |
| 2 |
故答案为:
| 2 |
| 2 |
点评:本题考查了坐标与图形变化-旋转,主要利用了旋转的性质,解直角三角形,锐角三角函数的定义,熟记性质是解题的关键,作出图形更形象直观,难点在于分情况讨论.

练习册系列答案
相关题目
702班某兴趣小组有7名成员,他们的年龄(单位:岁)分别为:12,13,13,14,12,13,15,则他们年龄的众数和中位数分别为( )
| A、13,14 |
| B、14,13 |
| C、13,13 |
| D、13,13.5 |
下列说法正确的是( )
| A、如果两个角相等,那么这两个角是对顶角 |
| B、有公共顶点的两个角是对顶角 |
| C、有公共顶点并且相等的两个角是对顶角 |
| D、如果两个角是对顶角,那么这两个角相等 |
 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C按顺时针方向旋转后得到△EDC,点D在AB边上,则△BCD的形状为
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C按顺时针方向旋转后得到△EDC,点D在AB边上,则△BCD的形状为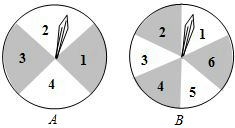 如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等份,每份分别标上1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1、2、3、4、5、6六个数字.有人为甲、乙两人设计了一个游戏,其规则如下:
如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等份,每份分别标上1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1、2、3、4、5、6六个数字.有人为甲、乙两人设计了一个游戏,其规则如下: