题目内容
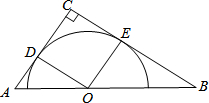 如图,在△ABC中,∠C=90°,点O在斜边AB上,以O为圆心的⊙O分别与AC,BC相切于点D,E,连接OD,OE.
如图,在△ABC中,∠C=90°,点O在斜边AB上,以O为圆心的⊙O分别与AC,BC相切于点D,E,连接OD,OE.(1)求证:四边形CDOE是正方形;
(2)当AC=4,BC=6时,求⊙O的半径.
考点:切线的性质,正方形的判定
专题:
分析:(1)先证明四边形ODCE为矩形,再根据OD=OE,可得出四边形CDOE为正方形;
(2)先设圆O的半径为r,再证明△OAD∽△BOE,即可得出圆O的半径.
(2)先设圆O的半径为r,再证明△OAD∽△BOE,即可得出圆O的半径.
解答:解:(1)∵AC、BC分别为半圆O的切线,
∴∠ODC=∠OEC=90°,
∵∠C=90°,
∴四边形ODCE为矩形,
∵OD=OE,
∴四边形CDOE为正方形;
(2)设⊙O的半径为r,
∵AC=4,BC=6,
∴AD=4-r,BE=6-r,
∵AC∥OE,
∴∠A=∠BOE,
∴△OAD∽△BOE,
∴
=
,
∴
=
,
解得r=2.4,
所以⊙O的半径为2.4.
∴∠ODC=∠OEC=90°,
∵∠C=90°,
∴四边形ODCE为矩形,
∵OD=OE,
∴四边形CDOE为正方形;
(2)设⊙O的半径为r,
∵AC=4,BC=6,
∴AD=4-r,BE=6-r,
∵AC∥OE,
∴∠A=∠BOE,
∴△OAD∽△BOE,
∴
| AD |
| OE |
| OD |
| BE |
∴
| 4-r |
| r |
| r |
| 6-r |
解得r=2.4,
所以⊙O的半径为2.4.
点评:本题考查了切线的性质以及正方形的判定,切线垂直于过切点的半径,三个角为直角且有一组邻边相等的四边形为正方形.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 如图,矩形ABCD中,BC=8,对角线BD=10,求tan∠ACB.
如图,矩形ABCD中,BC=8,对角线BD=10,求tan∠ACB.
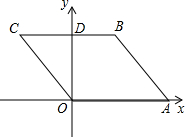 如图,菱形OABC的面积为
如图,菱形OABC的面积为