题目内容
12.(1)化简:$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$+$\frac{{x}^{2}+2x}{{x}^{2}+x-2}$.(2)解分式方程:$\frac{x-2}{x+2}$=$\frac{x+2}{x-2}$+$\frac{16}{{x}^{2}-4}$.
分析 (1)原式两项约分后,通分并利用同分母分式的加法法则计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=$\frac{(x+1)(x-1)}{(x-1)^{2}}$+$\frac{x(x+2)}{(x+2)(x-1)}$=$\frac{x+1}{x-1}$+$\frac{x}{x-1}$=$\frac{2x+1}{x-1}$;
(2)去分母得:x2-4x+4=x2+4x+4+16,
解得:x=-2,
经检验x=-2是增根,分式方程无解.
点评 此题考查了分式的加减法,以及解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.9的平方根是( )
| A. | 3 | B. | ±3 | C. | ±$\sqrt{3}$ | D. | ±81 |
20.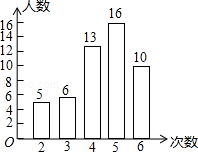 我市开展了“寻找雷锋足迹”的活动,某中学为了了解八年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了八年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,估计该校八年级800名学生在“学雷锋活动月”中做好事不少于5次的人数有( )
我市开展了“寻找雷锋足迹”的活动,某中学为了了解八年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了八年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,估计该校八年级800名学生在“学雷锋活动月”中做好事不少于5次的人数有( )
 我市开展了“寻找雷锋足迹”的活动,某中学为了了解八年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了八年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,估计该校八年级800名学生在“学雷锋活动月”中做好事不少于5次的人数有( )
我市开展了“寻找雷锋足迹”的活动,某中学为了了解八年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了八年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,估计该校八年级800名学生在“学雷锋活动月”中做好事不少于5次的人数有( )| A. | 384 | B. | 256 | C. | 160 | D. | 416 |
4.若方程组$\left\{\begin{array}{l}{2x+y=k+1}\\{x+2y=3}\end{array}\right.$的解x,y满足0<x+y<1,则k的取值范围是( )
| A. | -1<k<0 | B. | -4<k<-1 | C. | 0<k<1 | D. | k>-4 |
1.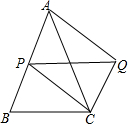 如图,在△ABC中,∠BAC=45°,AB=AC=8,P为AB边上一动点,以PA、PC为边作平行四边形PAQC,则对角线PQ的最小值为( )
如图,在△ABC中,∠BAC=45°,AB=AC=8,P为AB边上一动点,以PA、PC为边作平行四边形PAQC,则对角线PQ的最小值为( )
 如图,在△ABC中,∠BAC=45°,AB=AC=8,P为AB边上一动点,以PA、PC为边作平行四边形PAQC,则对角线PQ的最小值为( )
如图,在△ABC中,∠BAC=45°,AB=AC=8,P为AB边上一动点,以PA、PC为边作平行四边形PAQC,则对角线PQ的最小值为( )| A. | 6 | B. | 8 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
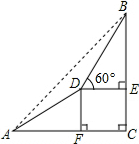 某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,如图所示,求山的高度BC.(结果精确到1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,如图所示,求山的高度BC.(结果精确到1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)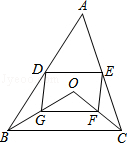 如图,点D,E分别是△ABC的边AB,AC的中点.点O是△ABC内的动点,点G,F分别是OB,OC的中点.
如图,点D,E分别是△ABC的边AB,AC的中点.点O是△ABC内的动点,点G,F分别是OB,OC的中点. 如图,直线AB∥CD,与直线EF分别交于M,N,则图中与∠END相等的角(∠END除外)的个数为( )
如图,直线AB∥CD,与直线EF分别交于M,N,则图中与∠END相等的角(∠END除外)的个数为( )