题目内容
7.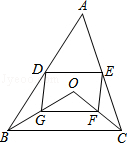 如图,点D,E分别是△ABC的边AB,AC的中点.点O是△ABC内的动点,点G,F分别是OB,OC的中点.
如图,点D,E分别是△ABC的边AB,AC的中点.点O是△ABC内的动点,点G,F分别是OB,OC的中点.(1)求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是正方形,请直接给出OA应满足的条件是AO=BC,AO⊥BC.
分析 (1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC且DE=$\frac{1}{2}$BC,GF∥BC且GF=$\frac{1}{2}$BC,从而得到DE∥GF且DE=GF,然后根据一组对边平行且相等的四边形是平行四边形;
(2)根据三角形的中位线平行于第三边并且等于第三边的一半,DG∥AO,DG=$\frac{1}{2}$AO,然后求出DG⊥GF,DG=GF,再根据邻边垂直且相等的平行四边形是正方形解答.
解答 (1)证明:∵D、E是AB、AC的中点,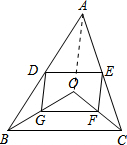
∴DE∥BC且DE=$\frac{1}{2}$BC,
∵G、F是OB、OC的中点,
∴GF∥BC且GF=$\frac{1}{2}$BC,
∴DE∥GF且DE=GF,
∴四边形DGFE是平行四边形;
(2)解:AO=BC,AO⊥BC时四边形DGFE是正方形,
理由如下:
∵D、G分别是AB、OB的中点,
∴DG∥AO,DG=$\frac{1}{2}$AO,
又∵AO=BC,AO⊥BC,
∴DG⊥GF,DG=GF,
∴四边形DGFE正方形,
故答案为:AO=BC,AO⊥BC.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,正方形的判定,熟记定理与判定方法是解题的关键.

练习册系列答案
相关题目
 解不等式$\frac{2x-3}{3}$≤$\frac{x-3}{5}$+1,并在数轴上表示其解集.
解不等式$\frac{2x-3}{3}$≤$\frac{x-3}{5}$+1,并在数轴上表示其解集.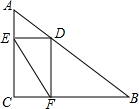 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )