题目内容
 分析探索题:细心观察如图,认真分析各式,然后解答问题.
分析探索题:细心观察如图,认真分析各式,然后解答问题.OA22=(
| 1 |
| ||
| 2 |
OA32=(
| 2 |
| ||
| 2 |
OA42=(
| 3 |
| ||
| 2 |
(1)请用含有n(n为正整数)的等式Sn=
(2)推算出OA10=
(3)求出 S12+S22+S32+…+S102的值.
考点:勾股定理,算术平方根
专题:规律型
分析:(1)此题要利用直角三角形的面积公式,观察上述结论,会发现,第n个图形的一直角边就是
,然后利用面积公式可得.
(2)由同述OA2=
,0A3=
…可知OA10=
.
(3)S12+S22+S32+…+S102的值就是把面积的平方相加就可.
| n |
(2)由同述OA2=
| 2 |
| 3 |
| 10 |
(3)S12+S22+S32+…+S102的值就是把面积的平方相加就可.
解答:解:(1)(
)2+1=n+1
Sn=
(n是正整数);
故答案是:
;
(2)∵OA12=1,
OA22=(
)2+1=2,
OA32=(
)2+1=3,
OA42=(
)2+1=4,
∴OA12=
,
OA2=
,
OA3=
,…
∴OA10=
;
故答案是:
;
(3)S12+S22+S32+…+S102
=(
)2+(
)2+(
)2+…+(
)2
=
(1+2+3+…+10)
=
.
即:S12+S22+S32+…+S102=
.
| n |
Sn=
| ||
| 2 |
故答案是:
| ||
| 2 |
(2)∵OA12=1,
OA22=(
| 1 |
OA32=(
| 2 |
OA42=(
| 3 |
∴OA12=
| 1 |
OA2=
| 2 |
OA3=
| 3 |
∴OA10=
| 10 |
故答案是:
| 10 |
(3)S12+S22+S32+…+S102
=(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 1 |
| 4 |
=
| 55 |
| 4 |
即:S12+S22+S32+…+S102=
| 55 |
| 4 |
点评:此题考查了勾股定理、算术平方根.解题的关键是观察,观察题中给出的结论,由此结论找出规律进行计算.千万不可盲目计算.

练习册系列答案
相关题目
 如图,∠ABD=∠ACD,图中相似三角形的对数是( )
如图,∠ABD=∠ACD,图中相似三角形的对数是( )| A、2 | B、3 | C、4 | D、5 |
下列图形是棱锥的是( )
A、 |
B、 |
C、 |
D、 |
数轴上表示整数的点称为整点.某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2014厘米的线段AB,则线段AB盖住的整点的个数是( )
| A、2014 |
| B、2015 |
| C、2014或2015 |
| D、2014和2015 |
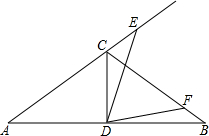 如图,在△ABC中,AC=BC,∠A=30°,D为AB的中点,∠EDF=60°,E,F分别在AC,BC上
如图,在△ABC中,AC=BC,∠A=30°,D为AB的中点,∠EDF=60°,E,F分别在AC,BC上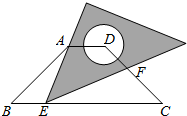 如图,在等腰梯形ABCD中,AD∥BC,BC=4
如图,在等腰梯形ABCD中,AD∥BC,BC=4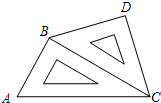 如图所示,把一副直角三角板摆放在一起,∠ACB=30°,∠BCD=45°,∠ABC=∠BDC=90°,量得CD=20CM,试求BC、AC的长.
如图所示,把一副直角三角板摆放在一起,∠ACB=30°,∠BCD=45°,∠ABC=∠BDC=90°,量得CD=20CM,试求BC、AC的长.