题目内容
8.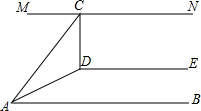 如图,已知AB∥DE∥MN,AD平分∠CAB,CD⊥DE.
如图,已知AB∥DE∥MN,AD平分∠CAB,CD⊥DE.(1)∠DAB=15°,求∠ACD的度数;
(2)判断等式∠CDA=∠NCD+∠DAB是否成立,并说明理由.
分析 (1)延长CD交AB于点F,根据AB∥DE∥MN,CD⊥DE可知CF⊥AB,再由AD平分∠CAB,∠DAB=15°求出∠CAF的度数,根据直角三角形的性质即可得出结论;
(2)延长ED交AC于点G,根据AB∥DE∥MN可知∠CDG=∠NCD,∠GDA=∠DAB,由此可得出结论.
解答 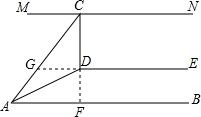 解:(1)延长CD交AB于点F,
解:(1)延长CD交AB于点F,
∵AB∥DE∥MN,CD⊥DE,
∴CF⊥AB.
∵AD平分∠CAB,∠DAB=15°,
∴∠CAF=30°,
∴∠ACD=90°-30°=60°;
(2)延长ED交AC于点G,
∵AB∥DE∥MN,
∴∠CDG=∠NCD,∠GDA=∠DAB,
∴∠CDA=∠NCD+∠DAB.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
相关题目
18.分式方程$\frac{2x-7}{x-2}$=1的解是( )
| A. | x=2 | B. | x=5 | C. | x=-1 | D. | x=1 |
16.在一次“交通安全法规”知识竞赛中,竞赛题共25道,每道题都给出四个答案,其中只有一个正确,选对得4分,不选或错选倒扣2分,得分不低于60分得奖,那么得奖至少应选对多少道题( )
| A. | 18 | B. | 19 | C. | 20 | D. | 21 |
3.已知$\frac{1}{a}$-$\frac{1}{b}$=2,则$\frac{ab}{a-b}$的值为( )
| A. | 0.5 | B. | -0.5 | C. | 2 | D. | -2 |
17.在直角坐标系内,点P(-3,5)关于x轴的对称点P1的坐标为( )
| A. | (3,-5) | B. | (3,5) | C. | (-3,5) | D. | (-3,-5) |