题目内容
18.计算:(1)解方程组$\left\{\begin{array}{l}{3(x+y)-2(x-y)=9}\\{(x+y)+2(x-y)=3}\end{array}\right.$
(2)解不等式组$\left\{\begin{array}{l}{3x<2x+4}\\{\frac{x+3}{3}-x≤-1}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)①+②×5得出16x=24,求出x,把x的值代入②求出y即可;
(2)先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:(1)整理得:$\left\{\begin{array}{l}{x+5y=9①}\\{3x-y=3②}\end{array}\right.$
①+②×5得:16x=24,
解得:x=$\frac{3}{2}$,
把x=$\frac{3}{2}$代入②得:$\frac{9}{2}$-y=3,
解得:y=$\frac{3}{2}$,
所以原方程组的解为:$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{3}{2}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x<2x+4①}\\{\frac{x+3}{3}-x≤-1②}\end{array}\right.$
∵解不等式①得:x<4,
解不等式②得:x≥-3,
∴不等式组的解集为-3≤x<4,
在数轴上表示不等式组的解集为: .
.
点评 本题考查了解二元一次方程组,解一元一次不等式组,在数轴上表示不等式组的解集的应用,能把二元一次方程组转化成一元一次方程是解(1)的关键,能求出不等式组的解集是解(2)的关键,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
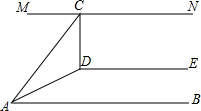 如图,已知AB∥DE∥MN,AD平分∠CAB,CD⊥DE.
如图,已知AB∥DE∥MN,AD平分∠CAB,CD⊥DE.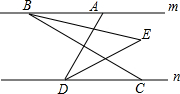 如图,已知直线m∥n,A、B是直线m上的任意两点,C、D是直线n上的任意两点,连AD、BC,∠ABC与∠ADC的平分线相交于点E,若∠BAD=80°.
如图,已知直线m∥n,A、B是直线m上的任意两点,C、D是直线n上的任意两点,连AD、BC,∠ABC与∠ADC的平分线相交于点E,若∠BAD=80°.
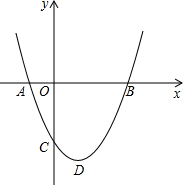 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中: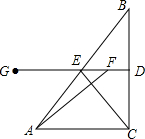 如图,在Rt△ABC中,∠ACB=90°,AC=4cm,动点F在BC的垂直平分线DG上,从D点出发以1cm/秒的速度移动,垂足为D,DG交AB于E,连接CE,设运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=4cm,动点F在BC的垂直平分线DG上,从D点出发以1cm/秒的速度移动,垂足为D,DG交AB于E,连接CE,设运动时间为t(s).