题目内容
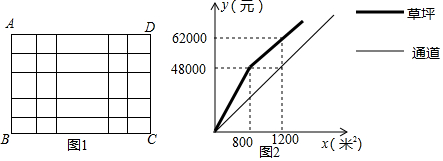
14.如图1,某校规划在一块长AD=60米,宽AB=40米的长方形ABCD空地上修建四条同样宽的通道,使其中两条与AB平行,另两条与AD平行,其余部分种花草.(1)要使草坪的面积为1500米2,求此时通道的宽应设计成多少米;
(2)已知某园林公司修建通道,草坪的造价分别为y1(元)、y2(元)与修建面积x(米2)之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,求通道宽为多少时,修建的通道和草坪的总造价最低,最低造价为多少元.
分析 (1)根据矩形面积公式列出列方程即可得到结论;
(2)根据图象,设出通道和花圃的解析式,用待定系数法求解,再根据实际问题写出自变量的取值范围即可.
解答 (1)设通道的宽应设计成a米,
根据题意得,(60-2a)(40-2a)=1500,
∴a1=5,a2=45(不合题意,舍去),
答:通道的宽为5米;
(2)设修建的道路和花圃的总造价为W,通道宽为a;
x花圃=(40-2a)(60-2a)=4a2-200a+2400;
x通道=60×40-(40-2a)(60-2a)=-4a2+200a,
由已知得y1=40(-4a2+200a),(2≤a≤10)
y2=$\left\{\begin{array}{l}{60x(0≤x<800)}\\{35x+20000(x≥800)}\end{array}\right.$
则W=y1+y2=$\left\{\begin{array}{l}{80{a}^{2}-4000a+144000(a=10)}\\{-20{a}^{2}+1000a+104000(2≤a<10)}\end{array}\right.$,
当a=2时,y有最小值,最小值为105920;
所以当通道宽为2米时,修建的通道和花圃的总造价最低为105920元.
点评 本题考查了一次函数的应用以及一元二次方程的应用,解题的关键是表示出花圃的长和宽.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.对于方程x2-2|x|+2=m,如果方程实根的个数为3个,则m的值等于( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2.5 |
 已知:一小球在如图所示正方形区域滚动,正方形ABCD边长为3,E、F、G、H分别为各边上的点,且AE=BF=CG=DH=1,则小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.
已知:一小球在如图所示正方形区域滚动,正方形ABCD边长为3,E、F、G、H分别为各边上的点,且AE=BF=CG=DH=1,则小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.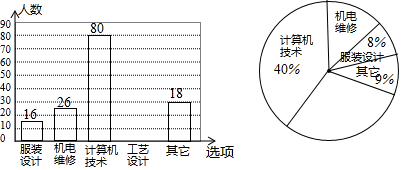
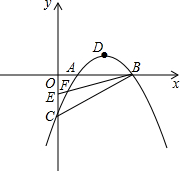 已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,-2),顶点为D,点E的坐标为(0,-1),该抛物线于BE交于另一点F,连接BC
已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,-2),顶点为D,点E的坐标为(0,-1),该抛物线于BE交于另一点F,连接BC