题目内容
已知二次函数的顶点坐标为(-
,-
),与y轴的交点为(0,n-m),其顶点恰好在直线y=x+
(1-m)上(其中m、n为正数).
(1)求证:此二次函数的图象与x轴有2个交点;
(2)在x轴上是否存在这样的定点:不论m、n如何变化,二次函数的图象总通过此定点?若存在,求出所有这样的点;若不存在,请说明理由.
| n |
| m+n |
| m2 |
| m+n |
| 1 |
| 2 |
(1)求证:此二次函数的图象与x轴有2个交点;
(2)在x轴上是否存在这样的定点:不论m、n如何变化,二次函数的图象总通过此定点?若存在,求出所有这样的点;若不存在,请说明理由.
考点:抛物线与x轴的交点
专题:证明题,存在型
分析:(1)把二次函数顶点坐标代入代入y=x+
(1-m)得-
+
(1-m)=-
,整理后利用因式分解得到(m-n)(m+1)=0,则m=n或m=-1(舍去),于是二次函数的顶点坐标为(-
,-
),与y轴的交点为(0,0),由m为正数可判断二次函数的顶点在第四象限,而抛物线过原点,所以抛物线开口向上,由此得到此二次函数的图象与x轴有2个交点;
(2)由(1)得到抛物线的对称轴为直线x=-
,抛物线与x轴的一个交点坐标为(0,0),利用对称性得到抛物线与x轴的另一个交点坐标为(-1,0).
| 1 |
| 2 |
| n |
| m+n |
| 1 |
| 2 |
| m2 |
| m+n |
| 1 |
| 2 |
| m |
| 2 |
(2)由(1)得到抛物线的对称轴为直线x=-
| 1 |
| 2 |
解答:(1)证明:把(-
,-
)代入y=x+
(1-m)得-
+
(1-m)=-
,
整理得m2-mn+m-n=0,
∵(m-n)(m+1)=0,
∴m=n或m=-1(舍去),
∴二次函数的顶点坐标为(-
,-
),与y轴的交点为(0,0),
∵m为正数,
∴二次函数的顶点在第四象限,
而抛物线过原点,
∴抛物线开口向上,
∴此二次函数的图象与x轴有2个交点;
(2)解:存在.
∵抛物线的对称轴为直线x=-
,抛物线与x轴的一个交点坐标为(0,0),
∴抛物线与x轴的另一个交点坐标为(-1,0),
即不论m、n如何变化,二次函数的图象总通过点(-1,0)和(0,0).
| n |
| m+n |
| m2 |
| m+n |
| 1 |
| 2 |
| n |
| m+n |
| 1 |
| 2 |
| m2 |
| m+n |
整理得m2-mn+m-n=0,
∵(m-n)(m+1)=0,
∴m=n或m=-1(舍去),
∴二次函数的顶点坐标为(-
| 1 |
| 2 |
| m |
| 2 |
∵m为正数,
∴二次函数的顶点在第四象限,
而抛物线过原点,
∴抛物线开口向上,
∴此二次函数的图象与x轴有2个交点;
(2)解:存在.
∵抛物线的对称轴为直线x=-
| 1 |
| 2 |
∴抛物线与x轴的另一个交点坐标为(-1,0),
即不论m、n如何变化,二次函数的图象总通过点(-1,0)和(0,0).
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标;二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
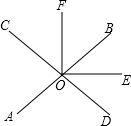 如图,直线AB与CD相交于点O,OE平分∠BOD,OF⊥OE于点O,若∠AOC=60°,求∠BOF的度数.
如图,直线AB与CD相交于点O,OE平分∠BOD,OF⊥OE于点O,若∠AOC=60°,求∠BOF的度数.