题目内容
 如图是圆心角为30°,半径分别是1、3、5、7、…的扇形组成的图形,阴影部分的面积依次记为S1、S2、S3、…,则Sn=
如图是圆心角为30°,半径分别是1、3、5、7、…的扇形组成的图形,阴影部分的面积依次记为S1、S2、S3、…,则Sn=考点:扇形面积的计算
专题:规律型
分析:由图可知S1=
,S2=
×3,S3=
×5,S4=
×7,…Sn=
×(2n-1),从而得出Sn的值.
| 8π |
| 12 |
| 8π |
| 12 |
| 8π |
| 12 |
| 8π |
| 12 |
| 8π |
| 12 |
解答:解:由题意可得出通项公式:Sn=
×(2n-1),
即Sn=
×(2n-1),
故答案为
.
| 8π |
| 12 |
即Sn=
| 2π |
| 3 |
故答案为
| 2(2n-1)π |
| 3 |
点评:本题考查了扇形面积的计算,是一道规律性的题目,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知三条线段长分别为a、b、c,a<b<c(a、b、c均为整数),若c=6,则线段a、b、c能组成三角形的情形有( )
| A、3种 | B、4种 | C、5种 | D、6种 |
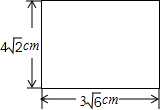 如图,已知一块矩形木板的长和宽分别为3
如图,已知一块矩形木板的长和宽分别为3| 6 |
| 2 |
下面的每组图形中,左面的平移后可以得到右面的是( )
A、 |
B、 |
C、 |
D、 |
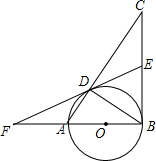 如图,在△ABC中,∠ABC=90°,AB=6,BC=8,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED并延长交BA的延长线于点F.
如图,在△ABC中,∠ABC=90°,AB=6,BC=8,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED并延长交BA的延长线于点F.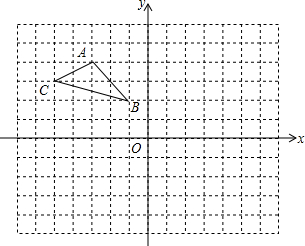 如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-1,2),C(-5,3).
如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-1,2),C(-5,3). 如图,在△ABC中,AB=AC=3cm,△BCN的周长是5cm,AB的垂直平分线交AC于点N,则BC=
如图,在△ABC中,AB=AC=3cm,△BCN的周长是5cm,AB的垂直平分线交AC于点N,则BC=