题目内容
11.若x是不等于1的有理数,我们把$\frac{1}{1-x}$称为x的差倒数,如2的差倒数是$\frac{1}{1-2}=-1$,-1的差倒数为$\frac{1}{1-(-1)}=\frac{1}{2}$,现已知${x}_{1}=\frac{1}{3}$,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数…则x2014=$\frac{1}{3}$.分析 按照求差倒数的方法,计算得出x1、x2、x3、x4…,找出循环的规律,进一步求得答案即可.
解答 解:∵${x}_{1}=\frac{1}{3}$,
x2=$\frac{1}{1-\frac{1}{3}}$=$\frac{3}{2}$,
x3=$\frac{1}{1-\frac{3}{2}}$=-2,
x4=$\frac{1}{1-(-2)}$=$\frac{1}{3}$,
…
∴以$\frac{1}{3}$,$\frac{3}{2}$,-2这三个数字依次不断循环,
∵2014÷3=671…1,
∴x2014=x1=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算的规律,利用规律,解决问题.

练习册系列答案
相关题目
1.由腾讯与大粤网联合发布的“广东2013年GDP十强区排行榜“出炉,深圳南山区以3206亿元GDP总量位居首位,福田区,龙岗区,宝安区和罗湖区也榜上有名,请你将南山区GDP总量(单位:亿元)用科学记数法来表示(保留3个有效数字)( )
| A. | 3.2×103 | B. | 3.20×103 | C. | 3.21×103 | D. | 3.2×104 |
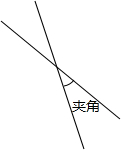 两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问:
两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问: