题目内容
3.已知抛物线y2=2x上有两点P(x1,y1)、Q(x2,y2),过PQ的中点M作x轴的平行线,交抛物线于R点,求证:S△PQR=$\frac{1}{16}$|y1-y2|3.分析 根据P、Q的坐标求得M的坐标,进而求得R的坐标,求得RM的值,然后根据S△PQR=$\frac{1}{2}$RM×|y1-y2|,代入即可证得结论.
解答 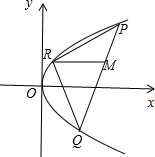 解:如图,∵P(x1,y1)、Q(x2,y2),M是PQ的中点,
解:如图,∵P(x1,y1)、Q(x2,y2),M是PQ的中点,
∴M点的坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$),
∵RM∥x轴,
∴R点的纵坐标为$\frac{{y}_{1}+{y}_{2}}{2}$,横坐标为x=$\frac{{y}^{2}}{2}$=$\frac{({y}_{1}+{y}_{2})^{2}}{8}$
∴RM=|$\frac{{x}_{1}+{x}_{2}}{2}$-$\frac{({y}_{1}+{y}_{2})^{2}}{8}$|=|$\frac{4{x}_{1}+4{x}_{2}-({y}_{1}+{y}_{2})^{2}}{8}$=|$\frac{2{{y}_{1}}^{2}+2{{y}_{2}}^{2}-({y}_{1}+{y}_{2})^{2}}{8}$|=$\frac{({y}_{1}-{y}_{2})^{2}}{8}$,
∵S△PQR=$\frac{1}{2}$RM×|y1-y2|,
∴S△PQR=$\frac{1}{2}$×$\frac{({y}_{1}-{y}_{2})^{2}}{8}$×|y1-y2|=$\frac{1}{16}$|y1-y2|3.
点评 本题考查了二次函数图象上点的坐标特征,求得R、M的坐标是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
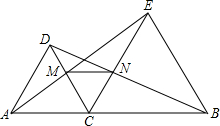 已知:如图,点C是线段AB上的动点(C点于A、B不重合),分别以AC、BC为边在直线AB的同侧作等边三角形ACD和等边三角形BCE,AE于CD相交于点M,BD与CE相交于点N.
已知:如图,点C是线段AB上的动点(C点于A、B不重合),分别以AC、BC为边在直线AB的同侧作等边三角形ACD和等边三角形BCE,AE于CD相交于点M,BD与CE相交于点N. ,按此规律
,按此规律 =-5.
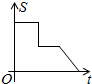
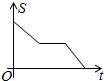
=-5.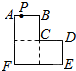 如图,三个大小相同的正方形ABCDEF拼成六边形,一动点P从点A出发沿着A→B→C→D→E方向匀速运动,最后到达点E.运动过程中△PEF的面积(s)随时间(t)变化的图象大致是( )
如图,三个大小相同的正方形ABCDEF拼成六边形,一动点P从点A出发沿着A→B→C→D→E方向匀速运动,最后到达点E.运动过程中△PEF的面积(s)随时间(t)变化的图象大致是( )
 已知:如图,以正方形ABCD的一边BC向正方形内作等边△EBC,则∠AEB=75°.
已知:如图,以正方形ABCD的一边BC向正方形内作等边△EBC,则∠AEB=75°.