题目内容
13.计算:$\frac{n}{m-n}$-$\frac{{n}^{3}}{{m}^{3}-2{m}^{2}n+m{n}^{2}}$÷$\frac{mn+{n}^{2}}{{m}^{2}-{n}^{2}}$.分析 首先对分式分子和分母分解因式,把除法转化为乘法,计算乘法,然后进行分式的减法运算即可.
解答 解:原式=$\frac{n}{m-n}$-$\frac{{n}^{3}}{m(m-n)^{2}}$•$\frac{(m+n)(m-n)}{n(m+n)}$
=$\frac{n}{m-n}$-$\frac{{n}^{2}}{m(m-n)}$
=$\frac{mn-{n}^{2}}{m(m-n)}$
=$\frac{n(m-n)}{m(m-n)}$
=$\frac{n}{m}$.
点评 本题考查了分式的混合运算,正确进行通分、因式分解和约分是解答的关键.

练习册系列答案
相关题目
1.给出下列表格:
根据表中信息,y关于x的函数解析式可以是y=3x-2.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -8 | -5 | -2 | 1 | 4 | … |
8.在直角坐标系内,下列结论成立的是( )
| A. | 点(4,3)与点(3,4)表示同一个点 | |
| B. | 平面内的任一点到两坐标轴的距离相等 | |
| C. | 若点P(x,y)的坐标满足xy=0,则点P在坐标轴上 | |
| D. | 点P(m,n)到x轴的距离为m,到y轴的距离为n |
 如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合)PM,PN分别垂直于CD,AB,垂足分别为M,N,若⊙O的半径长度为2,则MN的长为$\sqrt{3}$.
如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合)PM,PN分别垂直于CD,AB,垂足分别为M,N,若⊙O的半径长度为2,则MN的长为$\sqrt{3}$.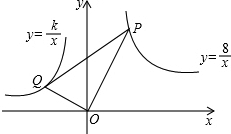 如果y=$\frac{8}{x}$过P点,y=$\frac{k}{x}$过Q点,OP⊥OQ,OP=2OQ,Q(m,1),则S△OPQ=5.
如果y=$\frac{8}{x}$过P点,y=$\frac{k}{x}$过Q点,OP⊥OQ,OP=2OQ,Q(m,1),则S△OPQ=5.