题目内容
 如图在△ABC中,AB=5,AC=3,BC=4,P从A点出发,沿射线AC运动,速度为每秒2个单位长度,Q点从C点出发,沿射线CB运动,速度为每秒1个单位长度,若点P,Q同时出发,经过时间t后,△PQC与△ABC相似,求运动时间.
如图在△ABC中,AB=5,AC=3,BC=4,P从A点出发,沿射线AC运动,速度为每秒2个单位长度,Q点从C点出发,沿射线CB运动,速度为每秒1个单位长度,若点P,Q同时出发,经过时间t后,△PQC与△ABC相似,求运动时间.考点:一元二次方程的应用,勾股定理的逆定理,相似三角形的性质
专题:几何动点问题
分析:根据已知求出PC=3-2t,再分两种情况讨论当△PQC∽△ABC和△PQC∽△BAC时,列出比例式,进行计算即可.
解答:解:∵AC=3,BC=4,AP=2t,CQ=t,
∴PC=3-2t,
当△PQC∽△ABC时,
=
,
即
=
,
∴t=
;
当△PQC∽△BAC时,
=
,
即
=
∴t=
;
答:运动的时间是
秒或
秒时,△PQC与△ABC相似.
∴PC=3-2t,
当△PQC∽△ABC时,
| CP |
| AC |
| CQ |
| CB |
即
| 3-2t |
| 3 |
| t |
| 4 |
∴t=
| 12 |
| 11 |
当△PQC∽△BAC时,
| CP |
| CB |
| CQ |
| CA |
即
| 3-2t |
| 4 |
| t |
| 3 |
∴t=
| 9 |
| 10 |
答:运动的时间是
| 12 |
| 11 |
| 9 |
| 10 |
点评:此题考查了相似三角形的性质,用到的知识点是相似三角形的对应变成比例,注意分两种情况讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,正方形ABCD中,过D作DE∥AC,∠ACE=30°,CA=CE,CE交AD于点F,求证:AE=AF.
如图,正方形ABCD中,过D作DE∥AC,∠ACE=30°,CA=CE,CE交AD于点F,求证:AE=AF. 如图,已知矩形ABCD的两条对角线相交于O,AB=4cm,∠AOB=60°,求此矩形的面积.
如图,已知矩形ABCD的两条对角线相交于O,AB=4cm,∠AOB=60°,求此矩形的面积. 在我校举行九年的级季篮球赛上,九年级(1)班的啦啦队队员,为了在明天的比赛中给本班同学加油助威,提前每人制作了一面同一规格的直角三角形彩旗.队员小明放学回家后,发现自己的彩旗破损了一角,他想重新制作一面彩旗.请你帮助小明,用直尺与圆规在作出一个与破损前完全一样的三角形(保留作图痕迹,不写作法).
在我校举行九年的级季篮球赛上,九年级(1)班的啦啦队队员,为了在明天的比赛中给本班同学加油助威,提前每人制作了一面同一规格的直角三角形彩旗.队员小明放学回家后,发现自己的彩旗破损了一角,他想重新制作一面彩旗.请你帮助小明,用直尺与圆规在作出一个与破损前完全一样的三角形(保留作图痕迹,不写作法). 如图,以格点为端点的线段叫格点线段,点A、B均在边长为1的网格的格点上,将格点线段AB先水平向左平移1个单位,再向上平移2个单位.
如图,以格点为端点的线段叫格点线段,点A、B均在边长为1的网格的格点上,将格点线段AB先水平向左平移1个单位,再向上平移2个单位.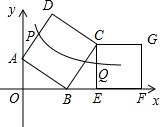 如图,正方形ABCD和正方形CEFG各有两个顶点在坐标轴上,其中A(0,1),B(2,0),E、F两点同在x轴上,双曲线y=
如图,正方形ABCD和正方形CEFG各有两个顶点在坐标轴上,其中A(0,1),B(2,0),E、F两点同在x轴上,双曲线y=