Question

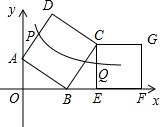如图，正方形ABCD和正方形CEFG各有两个顶点在坐标轴上，其中A（0，1），B（2，0），E、F两点同在x轴上，双曲线y=

k

x

（k＞0）经过边CE的中点Q．
（1）求证：△AOB≌△BEC；   
（2）求该双曲线所表示的函数关系式．

Answer 1

考点：反比例函数综合题

专题：

分析：（1）根据ASA定理可得出结论；
（2）根据（1）中△AOB≌△BEC可得出BE、CE的长，由Q是CE的中点得出Q点的坐标，进而可得出k的值，从而得出结论．

解答：解：（1）∵四边形ABCD是正方形，
∴AB=BC，∠ABC=90°，
∵∠OAB+∠ABO=90°，∠ABO+∠CBE=90°，∠CBE+∠BCE=90°，
∴∠OAB=∠CBE，∠ABO=∠BCE，
在△AOB与△BEC中，
∵

∠OAB=∠CBE AB=BC ∠ABO=∠BCE

，
∴△AOB≌△BEC；

（2）∵A（0，1），B（2，0），
∴OA=1，OB=2，
∵由（1）知△AOB≌△BEC，
∴OA=BE=1，OB=CE=2，
∴E（3，0），C（3，2），
∵Q是CE的中点，
∴Q（3，1），
∵点Q在反比例函数y=

k

x

上，
∴k=1×3=3，
∴反比例函数的关系是为y=

3

x

．

点评：本题考查的是反比例函数综合题，熟知正方形的性质及反比例函数图象上点的坐标特点是解答此题的关键．