题目内容
5.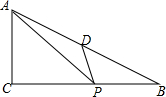 如图,Rt△ABC中,∠C=90°,∠B=30°,BC=8,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是8.
如图,Rt△ABC中,∠C=90°,∠B=30°,BC=8,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是8.
分析 作A关于BC的对称点A',连接A′B,易求∠A=60°,则PA=A'P,且△AA'B为等边三角形,AP+DP=A'P+PD为A'与直线AB之间的连接线段,其最小值为A'到AB的距离=BC=8,所以最小值为8.
解答 解:作A关于BC的对称点A',连接A′B,
∵∠C=90°,∠B=30°,
∴∠A=60°,
∵PA=A'P,
∴△AA'B为等边三角形,
∴AP+DP=A'P+PD为A'与直线AB之间的连接线段,
∴最小值为A'到AB的距离=BC=8,
故答案为:8.
点评 本题考查的是最短线路问题及等边三角形的性质,熟知两点之间线段最短的知识是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.在一所有900名学生的学校随机调查了100人,其中有75人上学前吃早餐,在这所学校里随便问一个人,上学之前吃过早餐的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
15.小芳有两根长度为4cm和9cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为( )的木条.
| A. | 5cm | B. | 3cm | C. | 12cm | D. | 17cm |
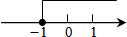
 如图所示,在数轴上点A所表示的数为a,则a的值为-1-$\sqrt{5}$.
如图所示,在数轴上点A所表示的数为a,则a的值为-1-$\sqrt{5}$.
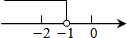
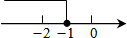
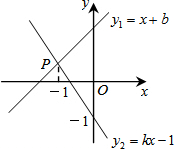 如图,已知直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b≤kx-1的解集在数轴上表示正确的是( )
如图,已知直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b≤kx-1的解集在数轴上表示正确的是( )
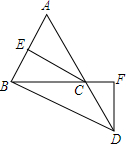 如图,在△ABC中,延长AC至点D,使CD=BC,连接BD,作CE⊥AB于点E,DF⊥BC交BC的延长线于点F,且AB=AC.如果∠ABD=105°,∠A=40度.
如图,在△ABC中,延长AC至点D,使CD=BC,连接BD,作CE⊥AB于点E,DF⊥BC交BC的延长线于点F,且AB=AC.如果∠ABD=105°,∠A=40度.