题目内容
7.先化简,再求值:$\frac{a-2}{{a}^{2}-1}$÷(a-1+$\frac{2a-1}{a+1}$),其中a是方程x2-x=6的根.分析 先解方程求得x的值,根据分式有意义的条件得到a的值,然后将a的值代入化简或所求代数式的值即可.
解答 解:解方程x2-x=6得到:x1=3,x2=-2,
因为a是方程x2-x=6的根,
所以a=3或a=-2.
$\frac{a-2}{{a}^{2}-1}$÷(a-1+$\frac{2a-1}{a+1}$),
=$\frac{a-2}{{a}^{2}-1}$÷$\frac{{a}^{2}-1+2a-1}{a+1}$,
=$\frac{a-2}{(a+1)(a-1)}$×$\frac{a+1}{{a}^{2}+2a-2}$,
=$\frac{a-2}{(a-1)({a}^{2}+2a-2)}$.
当a=3时,原式=$\frac{3-2}{(3-1)({3}^{2}+6-2)}$=$\frac{1}{26}$.
当a=-2时,原式=$\frac{-2-2}{(-2-1)(4-4-2)}$=-$\frac{2}{3}$.
点评 本题考查了分式的化简求值,一元二次方程的解,解答一元二次方程时可以采用因式分解法.

练习册系列答案
相关题目
17.使二次根式$\sqrt{\frac{3}{x-1}}$有意义的x的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x≤1 | D. | x≥1 |
15.关于x的一元二次方程x2-ax-1=0的两根之和为4,则a=( )
| A. | 1 | B. | -1 | C. | -4 | D. | 4 |
17.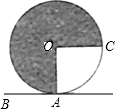 如图,⊙O的半径是1,AB是⊙O的切线,A是切点,若半径OC∥AB,则阴影部分的面积为( )
如图,⊙O的半径是1,AB是⊙O的切线,A是切点,若半径OC∥AB,则阴影部分的面积为( )
 如图,⊙O的半径是1,AB是⊙O的切线,A是切点,若半径OC∥AB,则阴影部分的面积为( )
如图,⊙O的半径是1,AB是⊙O的切线,A是切点,若半径OC∥AB,则阴影部分的面积为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
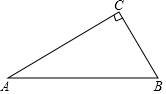 如图,△ABC中,∠C=90°,∠A=30°
如图,△ABC中,∠C=90°,∠A=30°