题目内容
15.若一元二次方程ax2+bx+c=0的一个根为1,且a、b满足等式b=$\sqrt{a-2}+\sqrt{2-a}$-1.(1)求出a、b、c分别是多少?
(2)求方程$\frac{1}{4}{y^2}$+c=0的解.
分析 (1)把x=1代入方程ax2+bx+c=0得到a+b+c=0,利用非负数的性质得到a和b的值,进而求出c的值;
(2)把c=-1代入方程$\frac{1}{4}{y^2}$+c=0,再利用直接开平方法求出方程的根.
解答 解:(1)∵1是一元二次方程ax2+bx+c=0的一个根,
∴a+b+c=0,
根据二次根式被开方数的非负数性可知:$\left\{\begin{array}{l}{a-2≥0}\\{2-a≥0}\end{array}\right.$解得:a=2;
把a=2代入b=0+0-1=-1; 把a=2,b=-1代入a+b+c=0解得:c=-1;
∴a=2,b=-1,c=-1.
(2)当c=-1时,$\frac{1}{4}{y^2}-1=0$;解得:y1=2,y2=-2.
点评 本题主要考查了一元二次方程的解以及直接开平方法求一元二次方程的根等知识点,解答本题的关键是根据非负数的性质求出a和b的值,此题难度不大.

练习册系列答案
相关题目
5.下列轴对称图形中,对称轴最多的是( )
| A. | 等腰直角三角形 | B. | 圆 | C. | 正方形 | D. | 正三角形 |
10.为了打造良好的校园学习环境,赵化中学用两年时间把校园种植花草树木的场地面积增加了69%,则这两年该校种植花草树木的场地面积平均每年增长率为( )
| A. | 34.5% | B. | 33% | C. | 30% | D. | 27% |
20.已知关于x的一元二次方程x2-ax-1=0(其中a为常数)的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 可能有实数根,也可能没有实数根 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
7.满足下列条件的△ABC不能构成直角三角形的一组是( )
| A. | ∠A=∠C-∠B | B. | ∠A:∠B:∠C=1:2:3 | C. | a2=(b+c)(b-c) | D. | a=1,b=2,c=3 |
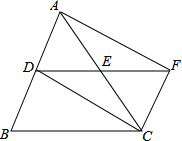 如图,△ABC中,DE是一条中位线,延长DE到点F,使EF=DE,连接CF.
如图,△ABC中,DE是一条中位线,延长DE到点F,使EF=DE,连接CF.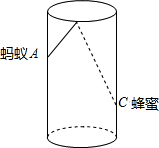 如图,圆柱形玻璃杯,高为8cm,底面周长为12cm,在杯内离杯底2cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,求蚂蚁到达蜂蜜的最短距离.
如图,圆柱形玻璃杯,高为8cm,底面周长为12cm,在杯内离杯底2cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,求蚂蚁到达蜂蜜的最短距离.