题目内容
 如图,已知:AD∥BC,AD=CB,AE=CF.求证:∠D=∠B.
如图,已知:AD∥BC,AD=CB,AE=CF.求证:∠D=∠B.
证明:∵AD∥BC,
∴∠A=∠________.
∵AE=CF,
∴AE+________=CF+________
∴AF=________.
在△AFD和△CEB中,
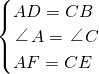
∴△AFD≌△CEB________.
∴∠D=∠B________.
C EF EF CE (SAS) 全等三角形的对应角相等
分析:由平行线的性质就可以得出∠A=∠C,在根据等式的性质就可以得出AF=CE,然后由SAS就可以得出△AFD≌△CEB,由全等三角形的性质就可以得出结论.
解答:由题意,得
:∵AD∥BC,
∴∠A=∠C.
∵AE=CF,
∴AE+EF=CF+EF
∴AF=CE.
在△AFD和△CEB中,
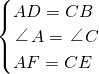
∴△AFD≌△CEB (SAS).
∴∠D=∠B (全等三角形的对应角相等).
故答案为:C;EF;EF;CE;SAS;全等三角形的对应角相等.
点评:本题考查了平行线的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时得出三角形全等是关键.
分析:由平行线的性质就可以得出∠A=∠C,在根据等式的性质就可以得出AF=CE,然后由SAS就可以得出△AFD≌△CEB,由全等三角形的性质就可以得出结论.
解答:由题意,得
:∵AD∥BC,
∴∠A=∠C.
∵AE=CF,
∴AE+EF=CF+EF
∴AF=CE.
在△AFD和△CEB中,
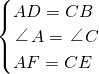
∴△AFD≌△CEB (SAS).
∴∠D=∠B (全等三角形的对应角相等).
故答案为:C;EF;EF;CE;SAS;全等三角形的对应角相等.
点评:本题考查了平行线的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时得出三角形全等是关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 12、如图,已知AC=AD,请增加一个条件,使△AEC≌△AED,这个条件是
12、如图,已知AC=AD,请增加一个条件,使△AEC≌△AED,这个条件是
 15、如图,已知AB=AD,在不添加任何辅助线的前提下,要使△ABC≌△ADC还需添加一个条件,这个条件可以是DC=BC.(只需写出一个)
15、如图,已知AB=AD,在不添加任何辅助线的前提下,要使△ABC≌△ADC还需添加一个条件,这个条件可以是DC=BC.(只需写出一个) 23、如图,已知:AD=BC,AC=BD.求证:OD=OC.
23、如图,已知:AD=BC,AC=BD.求证:OD=OC. 如图,已知:AD∥BC,且DC⊥AD于D,求证:
如图,已知:AD∥BC,且DC⊥AD于D,求证: