题目内容
2.已知|x-3|+(y-5)2+z2-8z+16=0,则以x,y,z为边的三角形面积为( )| A. | 4 | B. | 6 | C. | 12 | D. | 不能确定 |
分析 由条件可求得x、y、z的值,再根据勾股定理的逆定理可判定其为直角三角形,可求得答案.
解答 解:
∵|x-3|+(y-5)2+z2-8z+16=0,
∴|x-3|+(y-5)2+(z-4)2=0,
∴x=3,y=5,z=4,
∵x2+z2=9+16=25=y2,
∴以x,y,z为边的三角形是以y为斜边的直角三角形,
∴三角形面积=$\frac{1}{2}$xz=$\frac{1}{2}$×3×4=6,
故选B.
点评 本题主要考查非负数的性质及直角三角形的判定,求得x、y、z的值是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.若△ABC的一个外角为60o,那么△ABC一定是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 等腰三角形 |
14.下列计算正确的是( )
| A. | (±$\frac{1}{4}$)2=$\frac{1}{2}$ | B. | ±($\sqrt{1\frac{9}{16}}$)=±1$\frac{1}{4}$ | C. | -$\sqrt{0.9}$=-0.3 | D. | $\sqrt{1{3}^{2}-{7}^{2}}$=6 |
11.长方形的周长为a cm,长为b cm,则长方形的宽为( )
| A. | (a-2b) cm | B. | ($\frac{a}{2}$-2b) cm | C. | $\frac{a-b}{2}$ cm | D. | $\frac{a-2b}{2}$ cm |
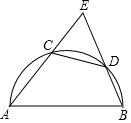 如图,C,D为半圆上的两点,且$\widehat{BD}$=$\widehat{DC}$,连接AC并延长,与BD的延长线相交于点E,写出图中相等的线段,并说明理由.
如图,C,D为半圆上的两点,且$\widehat{BD}$=$\widehat{DC}$,连接AC并延长,与BD的延长线相交于点E,写出图中相等的线段,并说明理由.
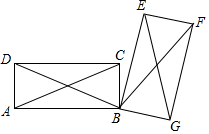 如图,把矩形ABCD绕点B顺时针旋转得到矩形EBGF,则图中与线段AC相等的线段有( )条.
如图,把矩形ABCD绕点B顺时针旋转得到矩形EBGF,则图中与线段AC相等的线段有( )条.