题目内容
如图，在Rt△ABC中，∠C=90°，AC=8，BC=15，以点C为圆心，AC为半径的⊙C交AB于点D，求AD的长．考点：垂径定理,勾股定理
专题：
分析：先根据勾股定理求出AB的长，过C作CM⊥AB，交AB于点M，由垂径定理可知M为AD的中点，由三角形的面积可求出CM的长，在Rt△ACM中，根据勾股定理可求出AM的长，进而可得出结论．
解答：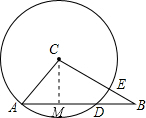
解：∵在Rt△ABC中，∠ACB=90°，AC=8，BC=15，
∴AB=
=
=17．
过C作CM⊥AB，交AB于点M，如图所示，
∵CM⊥AB，
∴M为AD的中点，
∵S△ABC=
AC•BC=
AB•CM，且AC=8，BC=15，AB=17，
∴CM=
=
，
在Rt△ACM中，根据勾股定理得：AC2=AM2+CM2，即64=AM2+（
）2，
解得：AM=
，
∴AD=2AM=
．
解：∵在Rt△ABC中，∠ACB=90°，AC=8，BC=15，∴AB=
| AC2+BC2 |
| 82+152 |
过C作CM⊥AB，交AB于点M，如图所示，
∵CM⊥AB，
∴M为AD的中点，
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CM=
| 8×15 |
| 17 |
| 120 |
| 17 |
在Rt△ACM中，根据勾股定理得：AC2=AM2+CM2，即64=AM2+（
| 120 |
| 17 |
解得：AM=
| 64 |
| 17 |
∴AD=2AM=
| 128 |
| 17 |
点评：本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
若分式
无意义，则a值的是（ ）
| a2-4 |
| a2-2a |
| A、0 | B、-2 | C、0或2 | D、±2 |
将抛物线y=（x-1）2+3向右平移1个单位，再向上平移3个单位后所得抛物线的表达式为（ ）
| A、y=（x-2）2 |
| B、y=x2 |
| C、y=x2+6 |
| D、y=（x-2）2+6 |
如图，在△ABC中，DE∥BC，DF∥AB，那么下列比例式中正确的是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将一副三角尺按如图所示的方式叠放在一起，则∠α的度数是（ ）| A、100° | B、120° |
| C、105° | D、不能确定 |