题目内容
在平面直角坐标系xOy中,抛物线y=ax2+c与x轴交于点A(-2,0)和点B,与y轴交于点C(0,2
),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.
(1)求该抛物线的解析式;
(2)在整个运动过程中,是否存在某一时刻,使得以A,P,Q为顶点的三角形与△AOC相似?如果存在,请求出对应的t的值;如果不存在,请说明理由.
(3)在y轴上有两点M(0,m)和N(0,m+1),若要使得AM+MN+NP的和最小,请直接写出相应的m、t的值以及AM+MN+NP的最小值.

| 3 |
(1)求该抛物线的解析式;
(2)在整个运动过程中,是否存在某一时刻,使得以A,P,Q为顶点的三角形与△AOC相似?如果存在,请求出对应的t的值;如果不存在,请说明理由.
(3)在y轴上有两点M(0,m)和N(0,m+1),若要使得AM+MN+NP的和最小,请直接写出相应的m、t的值以及AM+MN+NP的最小值.

考点:二次函数综合题
专题:
分析:(1)利用等定系数法求出抛物线的解析式即可,
(2)先求出AO,OC和AC,分两种情况①若∠APQ=90° 则cos∠CAO=cos∠PAQ,②若∠AQP=90°,则cos∠CAO=cos∠PAO,求解.
(3)先证出当AF是BC边上的高时,M是AF和y轴的交点AM+NP+MN有最小值,再利用∠DAB=30°求出m的值,利用RT△CPN求出CP,再求出t,最后得出AM+MN+NP的最小值.
(2)先求出AO,OC和AC,分两种情况①若∠APQ=90° 则cos∠CAO=cos∠PAQ,②若∠AQP=90°,则cos∠CAO=cos∠PAO,求解.
(3)先证出当AF是BC边上的高时,M是AF和y轴的交点AM+NP+MN有最小值,再利用∠DAB=30°求出m的值,利用RT△CPN求出CP,再求出t,最后得出AM+MN+NP的最小值.
解答:解:(1)把A(-2,0)和C(0,2
)代入y=ax2+c得
,
解得
.
∴抛物线的解析式为:y=-
x2+2
,
(2)在y=-
x2+2
中,
令y=0.则-
x2+2
=0,
解得,x1=-2,x2=2,
∴AB=4,
∵AP=t,AQ=4-2t,
在RT△AOC中,AO=2,OC=2
,
∴AC=
=
=4,
∴cos∠CAO=
=
,
①若∠APQ=90° 则cos∠CAO=cos∠PAQ,
∴
=
,
∴
=
,
解得t=1,
②若∠AQP=90°,则cos∠CAO=cos∠PAO,
∴
=
,
∴
=
,
解得t=
,
∴当t=1或t=
时,以A,P,Q为顶点的三角形与△AOC相似.
(3)如图1,作PN⊥AC,P′N⊥BC,垂足分别为P,P′,

∵抛物线的对称轴是y轴,
∴CO是∠ACB的角平分线,
∴NP=NP′,
作MF⊥BC.P′H∥MN,
∴四边形MHP′N是平行四边形,
∴MH=NP′=NP,P′H=MN,
由(1)可知,∠CAO=60°,
∴∠OCB=∠OCA=30°,
∴∠CMF=60°,
∴∠P′HF=60°,
∴HF=
P′H=
MN=
,
∴AM+NP=AM+MH>AF-
,
∴当AF是BC边上的高时,M是AF和y轴的交点,AM+NP有最小值,即AM+NP+MN有最小值,
如图2,作AD⊥BC于点D,

∵△ABC是正三角形,
∴∠DAB=30°,AO=2,
∴OM=
,
∴m=
,
∴CN=OC-ON=2
-
-1=
-1
在RT△CPN中∠NCP=30°,
∴PC=2-
,PN=
(
-1)=
-
∴AP=4-(2-
)=2+
∴t=2+
,
∴AM+MN+NP的最小值=
+1+
-
=2
+
.
| 3 |
|
解得
|
∴抛物线的解析式为:y=-
| ||
| 2 |
| 3 |
(2)在y=-
| ||
| 2 |
| 3 |
令y=0.则-
| ||
| 2 |
| 3 |
解得,x1=-2,x2=2,
∴AB=4,
∵AP=t,AQ=4-2t,
在RT△AOC中,AO=2,OC=2
| 3 |
∴AC=
| AO2+OC2 |
22+(2
|
∴cos∠CAO=
| AO |
| AC |
| 1 |
| 2 |
①若∠APQ=90° 则cos∠CAO=cos∠PAQ,
∴
| 1 |
| 2 |
| AP |
| AQ |
∴
| 1 |
| 2 |
| t |
| 4-2t |
解得t=1,
②若∠AQP=90°,则cos∠CAO=cos∠PAO,
∴
| 1 |
| 2 |
| AQ |
| AP |
∴
| 1 |
| 2 |
| 4-2t |
| t |
解得t=
| 8 |
| 5 |
∴当t=1或t=
| 8 |
| 5 |
(3)如图1,作PN⊥AC,P′N⊥BC,垂足分别为P,P′,

∵抛物线的对称轴是y轴,
∴CO是∠ACB的角平分线,
∴NP=NP′,
作MF⊥BC.P′H∥MN,
∴四边形MHP′N是平行四边形,
∴MH=NP′=NP,P′H=MN,
由(1)可知,∠CAO=60°,
∴∠OCB=∠OCA=30°,
∴∠CMF=60°,
∴∠P′HF=60°,
∴HF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AM+NP=AM+MH>AF-
| 1 |
| 2 |
∴当AF是BC边上的高时,M是AF和y轴的交点,AM+NP有最小值,即AM+NP+MN有最小值,
如图2,作AD⊥BC于点D,

∵△ABC是正三角形,
∴∠DAB=30°,AO=2,
∴OM=
2
| ||
| 3 |
∴m=
2
| ||
| 3 |
∴CN=OC-ON=2
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
在RT△CPN中∠NCP=30°,
∴PC=2-
| ||
| 2 |
| 1 |
| 2 |
4
| ||
| 3 |
2
| ||
| 3 |
| 1 |
| 2 |
∴AP=4-(2-
| ||
| 2 |
| ||
| 2 |
∴t=2+
| ||
| 2 |
∴AM+MN+NP的最小值=
4
| ||
| 3 |
2
| ||
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
点评:本题主要考查了二次函数的综合题,解题的关键是根据图形证出M在什么位置时AM+NP+MN有最小值.

练习册系列答案
相关题目
 如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.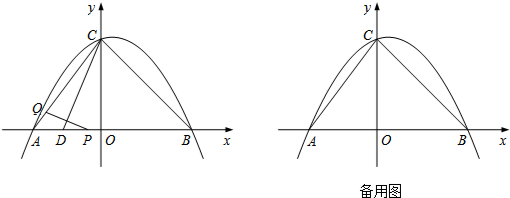
 已知:一次函数y=kx+b的图象过点(-1,3),(3,1).
已知:一次函数y=kx+b的图象过点(-1,3),(3,1). 七(1)班同学为了解2013年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.
七(1)班同学为了解2013年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.