题目内容
10. 如图,已知:等边△ABC边长为4cm,AD⊥BC于点D,求△ABC的面积.
如图,已知:等边△ABC边长为4cm,AD⊥BC于点D,求△ABC的面积.
分析 根据三角形的面积公式,求出即可.
解答 解:∵等边△ABC的边长4cm,AD是BC边上的高,
∴BD=CD=$\frac{1}{2}$BC=2cm,
∴根据勾股定理得:AD=$\sqrt{A{B}^{2}-B{D}^{2}}=\sqrt{{4}^{2}-{2}^{2}}=2\sqrt{3}$cm;
∵BC=4cm,AD=2$\sqrt{3}$cm,
∴S△ABC=$\frac{1}{2}$BC×AD=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$cm2.
点评 本题主要考查了等边三角形的性质,学生应掌握等边三角形的性质和熟练应用勾股定理.

练习册系列答案
相关题目
20.下面调查中,适合采用全面调查的是( )
| A. | 调查全国中学生心理健康现状 | B. | 调查你所在的班级同学的身高情况 | ||
| C. | 调查我市食品合格情况 | D. | 调查某电视台《第一时间》收视率 |
18.以下列各组数为边长,不能构成直角三角形的是( )
| A. | 1、2、$\sqrt{5}$ | B. | 1、$\sqrt{3}$、2 | C. | 3、4、5 | D. | 6、8、12 |
5.已知数据x1、x2、x3的平均数为m,数据y1、y2的平均数为n,那么数据x1、x2、x3、y1、y2的平均数为( )
| A. | m+n | B. | $\frac{m+n}{2}$ | C. | $\frac{m+n}{5}$ | D. | $\frac{3m+2n}{5}$ |
15.下列分式中最简分式为( )
| A. | $\frac{4}{2x}$ | B. | $\frac{2x}{{x}^{2}+1}$ | C. | $\frac{x-1}{{x}^{2}-1}$ | D. | $\frac{1-x}{x-1}$ |
20.已知一次函数y=ax+b在平面直角坐标系中的图案经过第一、二、三象限,则下列对a、b的符号判断正确的是( )
| A. | a<0,b<0 | B. | a>0,b>0 | C. | a>0,b<0 | D. | a<0,b>0 |
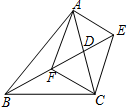 如图,在△ABC中,BD是AC边上的中线,F是BD上的一点,过点C作CE∥AF,交BD的延长线于点E.
如图,在△ABC中,BD是AC边上的中线,F是BD上的一点,过点C作CE∥AF,交BD的延长线于点E.