题目内容
15.为配合我市创建省级文明城市,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图.(1)该年级共有20个班,平均每班有4个文明行为劝导志愿者?并将条形图补充完整;
(2)该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率.
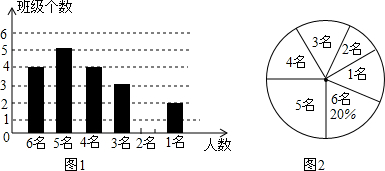
分析 (1)根据志愿者有6名的班级占20%,可求得班级总数,再求得志愿者是2名的班数,进而可求出每个班级平均的志愿者人数;
(2)由(1)得只有2名志愿者的班级有2个,共4名学生.设A1,A2来自一个班,B1,B2来自一个班,列出树状图可得出来自一个班的共有4种情况,则所选两名志愿者来自同一个班级的概率.
解答 解:(1)∵有6名志愿者的班级有4个,
∴班级总数为:4÷20%=20(个),
有两名志愿者的班级有:
20-4-5-4-3-2=2(个),如图所示:
该年级平均每班有;$\frac{1}{20}$(4×6+5×5+4×4+3×3+2×2+2×1)=4(名),
故答案为:20,4;
(2)由(1)得只有2名文明行为劝导志愿者的班级有2个,共4名学生.设A1,A2来自一个班,B1,B2来自一个班,
由树状图可知,共有12种可能的情况,并且每种结果出现的可能性相等,其中来自一个班的共有4种情况,
则所选两名文明行为劝导志愿者来自同一个班级的概率为:$\frac{4}{12}$=$\frac{1}{3}$.
点评 此题主要考查了条形统计图与扇形统计图的综合应用以及树状图法求概率,根据图象得出正确信息是解题关键.

练习册系列答案
相关题目
10.化简($\frac{x+y}{2}$)2+($\frac{x-y}{2}$)2,得( )
| A. | $\frac{{x}^{2}+{y}^{2}}{2}$ | B. | $\frac{{x}^{2}+{y}^{2}}{4}$ | C. | x2+y2 | D. | 2xy |
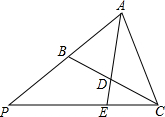 如图,在△ABC中,D为BC边上的中点,延长AD至E,使AD=2DE,连接CE并延长交AB的延长线于P,求$\frac{AB}{AP}$的值.
如图,在△ABC中,D为BC边上的中点,延长AD至E,使AD=2DE,连接CE并延长交AB的延长线于P,求$\frac{AB}{AP}$的值.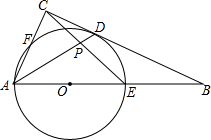 在Rt△ABC中,∠ACB=90°,O在AB上,⊙经过点A,与CB切于D,分别交AB、AC于E、F.
在Rt△ABC中,∠ACB=90°,O在AB上,⊙经过点A,与CB切于D,分别交AB、AC于E、F.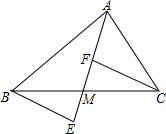 如图,M是△ABC的边BC上一点,△BME旋转后能与△CMF重合,已知∠ABC=∠ACF,∠EBM=28°,∠ACB=66°,求∠BAC的度数.
如图,M是△ABC的边BC上一点,△BME旋转后能与△CMF重合,已知∠ABC=∠ACF,∠EBM=28°,∠ACB=66°,求∠BAC的度数.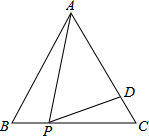 如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=$\frac{2}{3}$,则△ABC的边长为3.
如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=$\frac{2}{3}$,则△ABC的边长为3.