题目内容
7.若a+b=5,ab=4.求:(1)a2+b2的值;
(2)(a-b)2的值;
(3)$\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}$的值.
分析 (1)首先根据完全平方公式将a2+b2用(a+b)与ab的代数式表示,然后把a+b,ab的值整体代入计算;
(2)首先根据完全平方公式将(a-b)2用(a+b)与ab的代数式表示,然后把a+b,ab的值整体代入计算;
(3)首先根据完全平方公式将$\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}$用(a+b)与ab的代数式表示,然后把a+b,ab的值整体代入计算.
解答 解:(1)因为a+b=5,ab=4,可得:a2+b2=(a+b)2-2ab=25-8=17;
(2)因为a+b=5,ab=4,可得:(a-b)2=(a+b)2-4ab=25-16=9;
(3)因为a+b=5,ab=4,可得$\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\frac{(\sqrt{a}-\sqrt{b})^{2}}{a-b}=\frac{a+b-2\sqrt{ab}}{a-b}=\frac{5-4}{3}$=$\frac{1}{3}$
点评 本题考查了完全平方公式,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.解此题的关键是要了解a2+b2与(a+b)2之间的联系.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
17.下列各式是一元一次方程的是( )
| A. | 3x-1=5 | B. | x-y=3 | C. | x+3 | D. | 3x+y=5 |
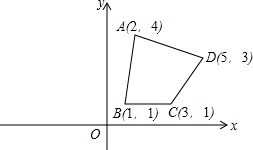 如图所示,四边形ABCD的顶点坐标分别为A(2,4)、B(1,1)、C(3,1)、D(5,3),请你补画出它关于y轴对称的图形A′B′C′D′,并写出顶点的坐标.
如图所示,四边形ABCD的顶点坐标分别为A(2,4)、B(1,1)、C(3,1)、D(5,3),请你补画出它关于y轴对称的图形A′B′C′D′,并写出顶点的坐标. 如图,长方形ABCD中,AD=8cm,CD=4cm.
如图,长方形ABCD中,AD=8cm,CD=4cm.