题目内容
5.用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.分析 工作效率:设A型机器人每小时搬大米x袋,则B型机器人每小时搬运(x-20)袋;工作量:A型机器人搬运700袋大米,B型机器人搬运500袋大米;工作时间就可以表示为:A型机器人所用时间=$\frac{700}{x}$,B型机器人所用时间=$\frac{500}{x-20}$,由所用时间相等,建立等量关系.
解答 解:设A型机器人每小时搬大米x袋,则B型机器人每小时搬运(x-20)袋,
依题意得:$\frac{700}{x}$=$\frac{500}{x-20}$,
解这个方程得:x=70
经检验x=70是方程的解,所以x-20=50.
答:A型机器人每小时搬大米70袋,则B型机器人每小时搬运50袋.
点评 本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.

练习册系列答案
相关题目
15.已知一组数据a,b,c的平均数为5,方差为4,那么数据a-2,b-2,c-2的平均数和方差分别是( )
| A. | 3,2 | B. | 3,4 | C. | 5,2 | D. | 5,4 |
16.-$\frac{1}{8}$的相反数是( )
| A. | 8 | B. | -8 | C. | $\frac{1}{8}$ | D. | -$\frac{1}{8}$ |
13.据相关报道,开展精准扶贫工作五年以来,我国约有55000000人摆脱贫困,将55000000用科学记数法表示是( )
| A. | 55×106 | B. | 0.55×108 | C. | 5.5×106 | D. | 5.5×107 |
20.若关于x、y的二元一次方程组$\left\{\begin{array}{l}x-y=2m+1\\ x+3y=3\end{array}\right.$的解满足x+y>0,则m的取值范围是m>-2.
3.化简x-{-x+[2x-(-x)]}的结果为( )
| A. | -x | B. | x | C. | 5x | D. | -5x |
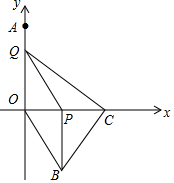 如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P、Q运动的时间为t(0<t<4)秒.
如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P、Q运动的时间为t(0<t<4)秒. 如图,利用热气球探测器测量大楼AB的高度,从热气球P处测得大楼B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离底面的高度为120m.试求大楼AB的高度(结果保留整数).
如图,利用热气球探测器测量大楼AB的高度,从热气球P处测得大楼B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离底面的高度为120m.试求大楼AB的高度(结果保留整数). BM平分∠ABC,∠A=20°,BC+CM=AB,求∠C的度数.
BM平分∠ABC,∠A=20°,BC+CM=AB,求∠C的度数.