题目内容
8. BM平分∠ABC,∠A=20°,BC+CM=AB,求∠C的度数.
BM平分∠ABC,∠A=20°,BC+CM=AB,求∠C的度数.
分析 在AB上截取BD=BC,求出AD=CM,利用“边角边”证明△BCD和△BCM全等,根据全等三角形对应边相等可得CM=DM,全等三角形对应角相等可得∠C=∠BDM,再求出AD=DM,根据等边对等角可得∠AMD=∠A,再利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答  解:如图,在AB上截取BD=BC,
解:如图,在AB上截取BD=BC,
∵BC+CM=AB,
BD+AD=AB,
∴AD=CM,
∵BM平分∠ABC,
∴∠ABM=∠CBM,
在△BCD和△BCM中,$\left\{\begin{array}{l}{BD=BC}\\{∠ABM=∠CBM}\\{BM=BM}\end{array}\right.$,
∴△BCD≌△BCM(SAS),
∴CM=DM,
∠C=∠BDM,
∴AD=DM,
∴∠AMD=∠A,
在△ADM中,由三角形的外角性质得,∠BDM=∠A+∠AMD=20°+20°=40°,
∴∠C=40°.
点评 本题考查了全等三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,等边对等角的性质,“截长补短”作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
3.微信根据移动ID所带来的数据,发布了“微信用户春节迁徙数据报告”,该报告显示,2016年1月24日春运首日至2月4日期间,人口流入最多的省份约有3 130 000微信用户在春节期间返乡.3 130 000用科学记数法可表示为( )
| A. | 3.13×102 | B. | 313×104 | C. | 3.13×105 | D. | 3.13×106 |
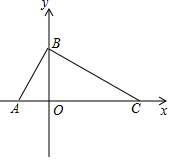 如图,在平面直角坐标系中,点A(-1,0),B(0,2),点C在x轴上,且∠ABC=90°.
如图,在平面直角坐标系中,点A(-1,0),B(0,2),点C在x轴上,且∠ABC=90°.