题目内容
19.(1)解方程:x2-4x-1=0;(2)解不等式组:$\left\{\begin{array}{l}{x-2(x-1)≤1}\\{\frac{1+x}{3}<x-1}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)利用配方法得到(x-2)2=5,然后利用直接开平方法解方程;
(2)分别解了两个不等式得到x≥1和x>2,然后根据同大取大确定不等式组的解集.
解答 解:(1)x2-4x=1,
x2-4x+4=5,
(x-2)2=5,
x-2=±$\sqrt{5}$,
所以x1=2+$\sqrt{5}$,x2=2-$\sqrt{5}$;
(2)$\left\{\begin{array}{l}{x-2(x-1)≤1①}\\{\frac{1+x}{3}<x-1②}\end{array}\right.$,
解①得x≥1,
解②得x>2,
所以不等式组的解集为x>2,
用数轴表示为:
点评 本题考查了解一元二次方程-配方法:将一元二次方程配成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.也考查了解一元一次不等式组.

练习册系列答案
相关题目
20.小苏和小林在如图1所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图2所示.下列叙述正确的是( )


| A. | 两人从起跑线同时出发,同时到达终点 | |
| B. | 小苏跑全程的平均速度大于小林跑全程的平均速度 | |
| C. | 小苏前15s跑过的路程大于小林前15s跑过的路程 | |
| D. | 小林在跑最后100m的过程中,与小苏相遇2次 |
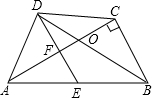 在四边形ABCD中,BD平分∠ABC,E为AB的中点,DE∥CB,∠ACB=90°,下面的结论中,正确的有①③④.①△BDE为等腰三角形,②∠AED=∠AOD,③AO•OC=DO•OB,④∠CAB=30°时,四边形BCDE为菱形.
在四边形ABCD中,BD平分∠ABC,E为AB的中点,DE∥CB,∠ACB=90°,下面的结论中,正确的有①③④.①△BDE为等腰三角形,②∠AED=∠AOD,③AO•OC=DO•OB,④∠CAB=30°时,四边形BCDE为菱形.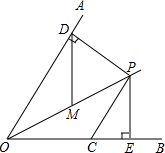 如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是$\sqrt{3}$.
如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是$\sqrt{3}$.