题目内容
 如图,BC⊥ED于O,∠A=27°,∠D=20°,则∠B=
如图,BC⊥ED于O,∠A=27°,∠D=20°,则∠B=考点:直角三角形的性质
专题:
分析:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BEO=∠A+∠D,再根据直角三角形两锐角互余列式计算即可求出∠B,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACB=∠D+∠COD.
解答:解:∵∠A=27°,∠D=20°,
∴∠BEO=∠A+∠D=27°+20°=47°,
∵BC⊥ED,
∴∠B=90°-∠BEO=90°-47°=53°;
在Rt△COD中,∠ACB=∠D+∠COD=29°+90°=110°.
故答案为:43°;110°.
∴∠BEO=∠A+∠D=27°+20°=47°,
∵BC⊥ED,
∴∠B=90°-∠BEO=90°-47°=53°;
在Rt△COD中,∠ACB=∠D+∠COD=29°+90°=110°.
故答案为:43°;110°.
点评:本题考查了直角三角形两锐角互余的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
若等腰三角形的周长为60cm,底边长为x cm,一腰长为y cm,则y与x的函数关系式及自变量x的取值范围是( )
| A、y=60-2x(0<x<60) | ||
| B、y=60-2x(0<x<30) | ||
C、y=
| ||
D、y=
|
若二次函数y=-(x-a)2+a-1的顶点在第四象限,则a的取值范围为( )
| A、a>1 | B、a<0 |
| C、0<a<1 | D、无法确定 |
 如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,AD和CE是高,它们相交于点H,求证:EH=EB.
如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,AD和CE是高,它们相交于点H,求证:EH=EB.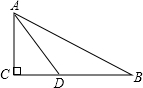 如图,在Rt△ABC中,∠BCA=90°,点D是BC上一点,AD=BD,若AB=8,BD=5,则CD=
如图,在Rt△ABC中,∠BCA=90°,点D是BC上一点,AD=BD,若AB=8,BD=5,则CD=